湖南省岳阳市华容县2023-2024学年七年级上学期期末数学试题
试卷更新日期:2024-02-20 类型:期末考试
一、选择题(本大题共8小题,每小题3分,满分24分,在每道小题给出的四个选项中,选出符合要求的一项)
-
1. 某自动控制器的芯片,可植入2020000000粒晶体管,这个数字2020000000用科学记数法可表示为A、 B、 C、 D、2. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则﹣3℃表示气温为( )A、零上3℃ B、零下3℃ C、零上7℃ D、零下7℃3. 如果|x|=2,那么x=( )A、2 B、﹣2 C、2或﹣2 D、2或4. 如图,在数轴上,点A、B分别表示a、b , 且 ,若 ,则点A表示的数为( )
 A、 B、0 C、3 D、5. 下列运算中,正确的是( ).A、 B、 C、 D、6. 下列调查中,适合于采用普查方式的是( )A、调查央视“春节联欢晚会”的收视率 B、了解外地游客对我县旅游景点的印象 C、了解一批新型节能灯的使用寿命 D、了解某中巴车上乘客的“健康码”情况7. 如图,是直角, , 则的度数是( )
A、 B、0 C、3 D、5. 下列运算中,正确的是( ).A、 B、 C、 D、6. 下列调查中,适合于采用普查方式的是( )A、调查央视“春节联欢晚会”的收视率 B、了解外地游客对我县旅游景点的印象 C、了解一批新型节能灯的使用寿命 D、了解某中巴车上乘客的“健康码”情况7. 如图,是直角, , 则的度数是( ) A、45° B、55° C、65° D、75°8. 一艘船从甲码头到乙码头顺流而行,全程需7个小时,逆流航行全程需要9小时,已知水流速度为每小时3千米.若设两个码头间的路程为x千米,则所列方程为( )A、 B、 C、 D、
A、45° B、55° C、65° D、75°8. 一艘船从甲码头到乙码头顺流而行,全程需7个小时,逆流航行全程需要9小时,已知水流速度为每小时3千米.若设两个码头间的路程为x千米,则所列方程为( )A、 B、 C、 D、二、填空题(本题共8小题,每小题4分,共32分)
-
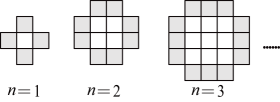
9. 比较大小:(填“>”或“<”).10. 如果与是同类项,那么 .11. 已知方程的解是 , 则 .12. 已知一个角是 , 则它的补角是 .13. 华容县为提倡节约用水,采取分段收费.若每户每月用水不超过20吨,每吨收费2元;若用水超过20吨,超过部分每吨加收1元.小明家5月份交水费52元,则他家该月用水吨.14. 已知 , 则.15. 已知 , , 为的平分线,则的度数为 .16. 当等于1、2、3时,由白色小正方形和黑色小正方形组成的图形如图,按此规律进行下去,当时,图形中白色小正方形和黑色小正方形的个数总和是个.第n个图形中白色小正方形和黑色小正方形的个数总和是个(用含n的代数式表示)
三、解答题(本大题共9小题,满分64分.解答应写出必要的文字说明、证明过程或演算步骤)
-
17. 已知多项式是关于x、y的五次四项式,单项式的次数为b,c是最小的正整数,求的值.18. 计算:(1)、;(2)、19. 先化简,再求值:
, 其中 , .
20. 解方程:(1)、(2)、21. 一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁.——程大位《直接算法统宗》意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?22. 某校在七年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调查.问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.请根据上述信息解答下列问题: (1)、该班参与问卷调查的人数有人;(2)、求C类人数占总调查人数的百分比;(3)、求扇形统计图中A类所对应扇形圆心角的度数.23. 如图所示,直线AB , CD相交于点O , 平分 , 射线在内部.
(1)、该班参与问卷调查的人数有人;(2)、求C类人数占总调查人数的百分比;(3)、求扇形统计图中A类所对应扇形圆心角的度数.23. 如图所示,直线AB , CD相交于点O , 平分 , 射线在内部.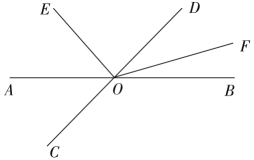 (1)、若 , 求的度数.(2)、若 , 求的度数.24. 列方程解应用题:
(1)、若 , 求的度数.(2)、若 , 求的度数.24. 列方程解应用题:快放寒假了,小宇来到书店准备购买一些课外读物在假期里阅读,在选完书结账时,收银员告诉小宇,如果花21元办理一张会员卡,用会员卡结账买书,可以享受7折优惠,小宇心算了一下,觉得这样可以节省18元,很合算,于是采纳了收银员的意见.请根据以上信息解答下列问题:
(1)、你认为小宇购买多少元以上的书,办卡就合算了;(2)、小宇购买这些书的原价是多少元?25. 如图,在数轴上点A表示的数是 , 点B在点的右侧,且到点的距离是18;点在点与点之间,且到点的距离是到点距离的2倍. (1)、点表示的数是;点表示的数是;(2)、若点从点出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点从点出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为秒,在运动过程中,当为何值时,点与点之间的距离为8?(3)、在(2)的条件下,若点与点之间的距离表示为 , 点与点之间的距离表示为 , 在运动过程中,是否存在某一时刻使得?若存在,请求出此时点表示的数:若不存在,请说明理由.
(1)、点表示的数是;点表示的数是;(2)、若点从点出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点从点出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为秒,在运动过程中,当为何值时,点与点之间的距离为8?(3)、在(2)的条件下,若点与点之间的距离表示为 , 点与点之间的距离表示为 , 在运动过程中,是否存在某一时刻使得?若存在,请求出此时点表示的数:若不存在,请说明理由.