湖南省株洲市炎陵县2023-2024学年八年级上学期期末数学试题

试卷更新日期：2024-02-20 类型：期末考试

进入出卷网下载

一、选择题（共10小题，每小题3分，满分30分）

1. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < 2$ B、 $x > 2$ C、 $x \leq 2$ D、 $x \geq 2$

查看试题解析
2. 下列式子中，为最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{2}$ C、 $\sqrt{4}$ D、 $\sqrt{12}$

查看试题解析
3. 若 $x > y$ ，则下列式子中错误的是（）

A、 $x - 1 > y - 1$ B、 $- 2 x > - 2 y$ C、 $x + 2 > y + 2$ D、 $\frac{x}{2022} > \frac{y}{2022}$

查看试题解析
4. 以下列各组线段为边，能构成三角形的是（）

A、1cm，2cm，3cm B、4cm，5cm，9cm C、3cm，4cm，5cm D、3cm，5cm，10cm

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{{(- \frac{3}{4})}^{2}} = - \frac{3}{4}$ C、 $2 \sqrt{3} - \sqrt{3} = \sqrt{3}$ D、 $\sqrt{9} = \pm 3$

查看试题解析
6. 解分式方程 $\frac{x}{3 x - 1} + \frac{3}{1 - 3 x} = 2$ 时，去分母化为一元一次方程，正确的是（）

A、 $x + 3 = 2$ B、 $x - 3 = 2$ C、 $x - 3 = 2 (3 x - 1)$ D、 $x + 3 = 2 (3 x - 1)$

查看试题解析
7. 下列命题中，是真命题的是（）

A、如果 $a c > b c$ ，那么 $a > b$ B、9的立方根是3 C、有一个角是 $60 °$ 的三角形是等边三角形 D、16的算术平方根是4

查看试题解析
8. 如图，用直尺和圆规作已知角的平分线的示意图，则说明∠CAD＝∠DAB的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
9.
如图，等腰三角形ABC中，AB=AC，BD是AC边上的高，若∠A=36°，则∠DBC的大小是（）

A、18° B、36° C、54° D、72°

查看试题解析
10. 两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积= $\frac{1}{2}$ AC•BD，其中正确的结论有（）

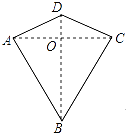A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题（本题共8小题，每小题3分，共24分）

11. 若分式 $\frac{x - 5}{x - 1}$ 的值为0，则x的值为．

查看试题解析
12. 不等式 $1 - 2 x \leq 4$ 的解集是．

查看试题解析
13. “手撕钢”厚度只有A4纸厚度的四分之一，我国某“手撕钢”团队，生产的钢材厚度降到了15微米．已知1微米 $= 0.000001$ 米，则15微米用科学记数法表示为米．

查看试题解析
14. 下列各数： $π$ ， $\sqrt{10}$ ， $\sqrt{25}$ ， $0.2$ ， $1.2020020002 \cdot \cdot \cdot$ （相邻的两个2之间依次多一个0）中，其中为有理数的是．（填写有理数）

查看试题解析
15. 如图，在△ABC中，AB=AC，边AB的垂直平分线MN交AC于点D，若△BCD的周长为24cm，BC=10cm，则AB的长为 cm．

查看试题解析
16. 等腰三角形的两边长分别为3cm和6cm，这个等腰三角形的周长为cm.

查看试题解析
17. 如图，点B ， E是等边三角形 $△ A C D$ 的边 $C D$ 所在直线上的两点，且 $B C = C D = D E$ ，则 $∠ B A E =$ 度．

查看试题解析
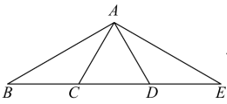18. 如图， $∠ 1 = ∠ 2$ ， $A B = A E$ ，添加一个条件，使得 $△ A B C ≌ △ Α E D$ ．

查看试题解析

三、解答题（本题共8小题，共66分）

19. 计算： ${(- \frac{1}{3})}^{- 2} + | 1 - \sqrt{2} | - {(π - 2)}^{0} + \sqrt{8}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} 2 x \geq - 2 ， \\ x + 3 < 4 ， \end{array}$ 并把不等式组的解集在数轴上表示出来．

查看试题解析
21. 解方程： $\frac{x}{x - 2} - \frac{x - 4}{2 - x}$ =3．

查看试题解析
22. 如图，已知 $E C = B F$ ， $A C = D F$ ， $∠ C = ∠ F$ ，求证： $△ C B A ≌ △ F E D$ ．

查看试题解析
23. 如图，△ABC中，AD⊥BC，点E在AC的垂直平分线上，且 BD=DE.

(1)、如果∠BAE= 40°，那么∠B=°　，∠C=°　；

(2)、如果△ABC的周长为13cm，AC=6cm，那么△ABE的周长=cm；

(3)、你发现线段AB与BD的和等于图中哪条线段的长，并证明你的结论．

查看试题解析
24. 先化简，再求值： $(1 - \frac{4}{x + 3}) \div \frac{x^{2} - 2 x + 1}{2 x + 6}$ ，其中 $x = \sqrt{2} + 1$ .

查看试题解析
25. 为支援灾区，某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件．已知B型学习用品的单价比A型学习用品的单价多10元，用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同．

(1)、求A、B两种学习用品的单价各是多少元？

(2)、若购买这批学习用品的费用不超过28000元，则最多购买B型学习用品多少件？

查看试题解析
26. 阅读理解
半角模型：半角模型是指有公共顶点，锐角等于较大角的一半，且组成这个较大角两边相等，通过翻折或旋转，将角的倍分关系转化为角的相等关系，并进一步构造全等三角形，使条件弱化，这样可把握问题的本质．

(1)、【问题背景】
如图1，在四边形 $A B C D$ 中， $A B = A D ， ∠ B A D = 120 ° ， ∠ B = ∠ A D C = 90 ° ， E 、 F$ 分别是 $B C 、 C D$ 上的点， $∠ E A F = 60 °$ ，试探究图1中线段 $B E 、 E F 、 F D$ 之间的数量关系．

(2)、【初步探索】
小亮同学认为解决此问题可以用如下方法：延长 $F D$ 到点 $G$ ，使 $D G = B E$ ，连接 $A G$ ，先证明 $△ A B E ≌ △ A D G$ ，再证明 $△ A E F ≌ △ A G F$ ，则可得到线段 $B E 、 E F 、 F D$ 之间的数量关系是．

(3)、【探索延伸】
如图2，在四边形 $A B C D$ 中， $A B = A D ， ∠ B + ∠ D = 180 °$ ， $E 、 F$ 分别是 $B C 、 C D$ 上的点， $∠ E A F = \frac{1}{2} ∠ B A D$ ，上述结论是否仍然成立，并说明理由．

(4)、【结论运用】
如图3，在某次军事演习中，舰艇甲在指挥中心（ $O$ 处）北偏西 $30 °$ 的 $A$ 处，舰艇乙在指挥中心南偏东 $70 °$ 的 $B$ 处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以 $60$ 海里/小时的速度前进，舰艇乙沿北偏东 $50 °$ 的方向以 $80$ 海里/小时的速度前进， $1.5$ 小时后，指挥中心观测到甲、乙两舰艇分别到达 $E 、 F$ 处，且两舰艇之间的夹角 $∠ E O F$ 为 $70 °$ ，则此时两舰艇之间的距离为海里．

查看试题解析