湖南省张家界市永定区2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-20 类型:期末考试
一、选择题(本大题共10个小题,每小题3分,满分30分.请将正确答案的字母代号填在下表中.)
-
1. 下列各数: , , , , , , 其中无理数有( )A、个 B、个 C、个 D、个2. 下列各式中不是分式的是( )A、 B、 C、 D、3. 若 , 则下列不等式成立的是( )A、 B、 C、 D、4. 下列式子正确的是( )A、 B、 C、 D、5. 如果三角形的两边分别为3和5,那么这个三角形的周长可能是A、15 B、16 C、8 D、76. 计算的结果为( )A、 B、 C、 D、7. 将一副直角三角板如图放置,使两直角边重合,则的度数为( )
 A、 B、 C、 D、8. 若关于x的方程有增根,则的值为( )A、 B、 C、0 D、19. a , b是两个连续整数,若 , 则是( )A、12 B、13 C、20 D、2110. 我国宋代数学家杨辉发现了( , 1,2,3,…)展开式系数的规律:
A、 B、 C、 D、8. 若关于x的方程有增根,则的值为( )A、 B、 C、0 D、19. a , b是两个连续整数,若 , 则是( )A、12 B、13 C、20 D、2110. 我国宋代数学家杨辉发现了( , 1,2,3,…)展开式系数的规律:
以上系数三角表称为“杨辉三角”,根据上述规律,展开式的系数和是( )
A、64 B、128 C、256 D、612二、填空题(本大题共8小题,每小题3分,满分24分)
-
11. 当x时,分式无意义.12. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005科学记数法表示为.13. 计算,并把结果化为只含有正整数指数幂的形式:= .14. 把命题“和为的两个角互为补角”写成“如果......,那么......”的形式是 .15. 已知不等式组无解,则m的取值范围是 .16. 如图所示, , , , , , 三点在一条直线上,若 , , 则的度数为.
 17. 对于三个数a , b , c , 我们规定表示这三个数中最大的数.例如 , 若 , 则x的取值范围是 .18. 如图,在中, , 平分 , 交于点 , 点、分别为、上的动点,若 , 的面积为 , 则的最小值为 .
17. 对于三个数a , b , c , 我们规定表示这三个数中最大的数.例如 , 若 , 则x的取值范围是 .18. 如图,在中, , 平分 , 交于点 , 点、分别为、上的动点,若 , 的面积为 , 则的最小值为 .
三、解答题(共66分)
-
19. 计算:(1)、;(2)、 .20. 解不等式组: , 并写出它的所有正整数解.21. 如图,∠1=∠2,AB=AE , AC=AD . 求证:BC=ED .
 22. 先化简,再求值: , 其中 .23. 已知 .(1)、求和的值;(2)、求的值;(3)、若的小数部分是 , 的整数部分是 , 求的值.24. 2022年12月26日常益长高铁全线开通,高铁的开通为张家界市民的出行带来了方便.从张家界到长沙,路程约为 , 某趟动车的平均速度比普通列车快 , 所需时间比普通列车少1小时,求该趟动车的平均速度.25. 阅读材料,并解决问题,我们知道,分子比分母小的分数叫做“真分数”,分子大于或等于分母的分数,叫做“假分数”.类似地,我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
22. 先化简,再求值: , 其中 .23. 已知 .(1)、求和的值;(2)、求的值;(3)、若的小数部分是 , 的整数部分是 , 求的值.24. 2022年12月26日常益长高铁全线开通,高铁的开通为张家界市民的出行带来了方便.从张家界到长沙,路程约为 , 某趟动车的平均速度比普通列车快 , 所需时间比普通列车少1小时,求该趟动车的平均速度.25. 阅读材料,并解决问题,我们知道,分子比分母小的分数叫做“真分数”,分子大于或等于分母的分数,叫做“假分数”.类似地,我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如 , 这样的分式就是假分式;再如 , 这样的分式就是真分式;
假分数可以化成(即)带分数的形式,类似的,假分式也可以化为带分式(整式与真分式的和或差)的形式.如: ,
再如:
这样,分式就被拆分成了带分式(即一个整式()与一个分式()的差)的形式.
(1)、判断:是真分式还是假分式?(填“真分式”或“假分式”);(2)、将“假分式”化成带分式的形式;(3)、思考:当x取什么整数时,分式的值为整数?26. 在中, , , 过点C作直线 , 于点M,于点N.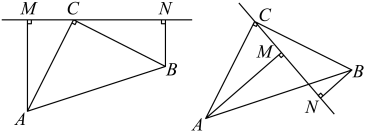 (1)、若在外(如图1),求证:;(2)、若与线段相交(如图2),且 , , 则 .
(1)、若在外(如图1),求证:;(2)、若与线段相交(如图2),且 , , 则 .