湖南省岳阳市华容县2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-20 类型:期末考试
一、选择题(本大题共10小题,每小题3分,满分30分.在每道小题给出的四个选项中,选出符合要求的一项)
-
1. 若分式有意义,则的取值范围是( )A、 B、 C、 D、2. 下列运算结果正确的是( )A、 B、 C、 D、3. 如图,为估计池塘岸边A、B间的距离,小方在池塘的一侧选取一点O , 米,米,A、B间的距离不可能是( )
 A、20米 B、23米 C、17米 D、26米4. 不等式 的解集在数轴上表示正确的是( )A、
A、20米 B、23米 C、17米 D、26米4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、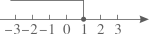 C、
C、 D、
D、 5. 若分式的的值同时扩大到原来的10倍,则此分式的值( )A、是原来的20倍 B、是原来的10倍 C、是原来的倍 D、不变6. 解分式方程 时,去分母化为一元一次方程,正确的是( )A、x+2=3 B、x﹣2=3 C、x﹣2=3(2x﹣1) D、x+2=3(2x﹣1)7. 下列命题的逆命题不成立的是( )A、全等三角形的对应角相等 B、线段垂直平分线上的点到线段两端的距离相等 C、三个角都是的三角形是等边三角形 D、负数没有平方根8. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、79. 已知 ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
5. 若分式的的值同时扩大到原来的10倍,则此分式的值( )A、是原来的20倍 B、是原来的10倍 C、是原来的倍 D、不变6. 解分式方程 时,去分母化为一元一次方程,正确的是( )A、x+2=3 B、x﹣2=3 C、x﹣2=3(2x﹣1) D、x+2=3(2x﹣1)7. 下列命题的逆命题不成立的是( )A、全等三角形的对应角相等 B、线段垂直平分线上的点到线段两端的距离相等 C、三个角都是的三角形是等边三角形 D、负数没有平方根8. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、79. 已知 ABC(AB<AC<BC),用尺规作图的方法在BC上取一点P,使PA+PC=BC,下列选项正确的是( )
A、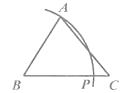 B、
B、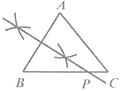 C、
C、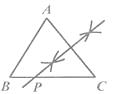 D、
D、 10. 如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )
10. 如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( ) A、∠ABC=2∠C B、∠ABC= ∠C C、 ∠ABC=∠C D、∠ABC=3∠C
A、∠ABC=2∠C B、∠ABC= ∠C C、 ∠ABC=∠C D、∠ABC=3∠C二、填空题(本大题共6小题,每小题3分,满分18分)
-
11. 64的算术平方根是.12. 肥皂泡沫的泡壁厚度大约是0.00075 mm,则数据0.00075用科学记数法表示为.13. 计算: .14. 若关于的方程有增根,则 .15. 若 , 则 .16. 已知关于 的不等式组 只有 个整数解,则实数 的取值范围是
三、解答题(本大题共9小题,满分72分)
-
17. 计算18. 解方程: .19. 解不等式组 , 并将解集在数轴上表示出来.
 20. 先化简,再求值: ,其中 .21. 如图,在△ABC中,点D为边AC上的一点,BD=BC,过点D作DE∥AB交BC于点E,且 DE平分∠BDC.
20. 先化简,再求值: ,其中 .21. 如图,在△ABC中,点D为边AC上的一点,BD=BC,过点D作DE∥AB交BC于点E,且 DE平分∠BDC.
求证:AD=BC.
22. 为了迎接在杭州举行的第19届亚运会,某旅游商店购进若干吉祥物钥匙扣和明信片,已知吉祥物钥匙扣的进价为18元/个,明信片的进价为6元/套,一个吉祥物钥匙扣的售价比一套明信片的售价高20元,若顾客花120元购买的吉祥物钥匙扣数量与花40元购买的明信片数量相同.(1)、求吉祥物钥匙扣和明信片的售价;(2)、为了促销,商店对吉祥物钥匙扣进行9折销售,某顾客同时购买吉祥物钥匙扣和明信片两种商品若干件,商家获毛利80元,请问有几种购买方案?23. 已知, , . 求值:(1)、;(2)、 .24. 如图,△ABC是等边三角形,点D在AC上,以BD为一边作等边△BDE,连接CE. (1)、说明△ABD ≌△CBE的理由;(2)、若∠BEC=82°,求∠DBC的度数.25. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.
(1)、说明△ABD ≌△CBE的理由;(2)、若∠BEC=82°,求∠DBC的度数.25. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题∶
 (1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.
(1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.