2024年浙教版数学八年级下册2.1一元二次方程课后培优练

试卷更新日期：2024-02-20 类型：同步测试

进入出卷网下载

一、选择题

1. 下列关于 $x$ 的方程：① $a x^{2} + b x + c = 0$ ；② $3 {(x - 9)}^{2} - {(x + 1)}^{2} = 1$ ；③ $x^{2} + \frac{1}{x} + 5 = 0$ ；④ $x^{2}$ $- 2 + 5 x^{3} - 6 = 0$ ；⑤ $3 x^{2} = 3 {(x - 2)}^{2}$ ；⑥ $12 x - 10 = 0$ .其中一元二次方程有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 把一元二次方程（1﹣x）（2﹣x）=3﹣x²化成一般形式ax²+bx+c=0（a≠0）其中a、b、c分别为（　　）

A、2、3、﹣1 B、2、﹣3、﹣1 C、2、﹣3、1 D、2、3、1

查看试题解析
3. 关于x的一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则a的值为（）

A、1 B、1或 $- 1$ C、 $- 1$ D、0.5

查看试题解析
4. 某放射性元素经2天后，质量衰变为原来的 $\frac{1}{2}$ ．若设这种放射性元素质量的日平均减少率为 $x$ ，则可列出方程为（）

A、 $1 - 2 x = \frac{1}{2}$ B、 $2 (1 - x) = \frac{1}{2}$ C、 $(1 - x)^{2} = \frac{1}{2}$ D、 $\frac{1}{2} (1 - x)^{2} = 1$

查看试题解析
5. 已知关于x的一元二次方程x²+3x-m=0的一个根是x=2，则m的值为（）

A、-10 B、-2 C、2 D、10

查看试题解析
6. 某市要组织一次篮球联赛，比赛制为单循环形式（每两队之间都赛一场），计划安排45场比赛，若设有 $x$ 支球队参加比赛，则所列方程正确的是（）

A、 $x (x - 1) = 45$ B、 $\frac{1}{2} x (x - 1) = 45$ C、 $x (x + 1) = 45$ D、 $\frac{1}{2} x (x + 1) = 45$

查看试题解析
7. 如图，在一块长为 $20 m$ ，宽为 $12 m$ 的矩形 $A B C D$ 空地内修建四条宽度相等，且与矩形各边垂直的道路，四条道路围成的中间部分恰好是一个正方形，且边长是道路宽的4倍，道路占地总面积为 $40 m^{2}$ ，设道路宽为 $x m$ ，则以下方程正确的是（）

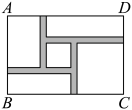A、 $32 x + 4 x^{2} = 4$ B、 $32 x + 8 x^{2} = 40$ C、 $64 x - 4 x^{2} = 40$ D、 $64 - 8 x^{2} = 40$

查看试题解析
8. 欧几里得的《原本》记载，形如x²+ax=b²的方程的图解法是：画Rt△ABC，使∠ACB=90°，BC= $\frac{a}{2}$ ，AC=b，再在斜边AB上截取BD= $\frac{a}{2}$ ，则该方程的一个正根是（）

A、AC的长 B、AD的长 C、BC的长 D、CD的长

查看试题解析

二、填空题

9. 已知一个一般形式的一元二次方程的二次项系数是 $\frac{1}{2}$ ，一次项系数是1，常数项是-2，则这个元二次方程是.

查看试题解析
10. 若关于x的一元二次方程x² +bx+c=0(b，c 为常数)的两根x₁ ， x₂满足-3<x₁<-1，1<x₂<3，则符合条件的一个方程为.

查看试题解析
11. 已知m是方程x²﹣2x﹣3＝0的一个根，则2m²﹣4m﹣1＝.

查看试题解析
12. 某网络学习平台2020年底的新注册用户数为100万，到2022年底的新注册用户数达到169万，设新注册用户数的年平均增长率为x，则可列出关于x的方程为．

查看试题解析

三、解答题

13. 向阳中学数学兴趣小组对关于x的方程（m+1） $x^{m^{2} + 1}$ +（m﹣2）x﹣1=0提出了下列问题：
（1）是否存在m的值，使方程为一元二次方程？若存在，求出m的值，并解此方程；
（2）是否存在m的值，使方程为一元一次方程？若存在，求出m的值，并解此方程．

查看试题解析
14. 已知x=2是关于x的一元二次方程x²+3x+m﹣2=0的一个根．
（1）求m的值及方程的另一个根；
（2）若7﹣x≥1+m（x﹣3），求x的取值范围

查看试题解析
15. 阅读理解题：
问题：已知方程x²+x-1=0，求一个一元二次方程，使它的根分别是已知方程的根的2倍．
解：设所求方程的根为y，则y=2x．
从而x= $\frac{y}{2}$
把x= $\frac{y}{2}$ 代人已知方程，得
( $\frac{y}{2}$ )²+ $\frac{y}{2}$ -1=0，
整理，得y²+2y-4=0，
因此，所求方程为y²+2y-4=0．
请你用上述思路解决下列问题：

(1)、已知方程x²+3x-2=0，求一个一元二次方程，使它的根分别为已知方程根的相反数；

(2)、已知关于x的一元二次方程ax²-bx+c=0(a≠0)有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

查看试题解析