【培优卷】2024年北师大版数学八（下）第一章三角形的证明章末检测

试卷更新日期：2024-02-19 类型：单元试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B \neq A C$ ．用无刻度的直尺和圆规在BC边上找一点D，使 $△ A C D$ 为等腰三角形．下列作法不正确的是（）

A、 B、 C、 D、

查看试题解析
2. $△ A B C$ 的三边长分别为 $a$ ， $b$ ， $c$ ．下列条件： $① ∠ A = ∠ B - ∠ C$ ； $② a^{2} = (b + c) (b - c)$ ； $③ ∠ A$ ∶ $∠ B$ ∶ $∠ C = 3$ ∶ $4$ ∶ $5$ ； $④ a$ ∶ $b$ ∶ $c = 5$ ∶ $12$ ∶ $13$ ．其中能判断 $△ A B C$ 是直角三角形的个数有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
3. 如图，在 $△ A B C$ 中， $A B = A C ， △ A B C$ 的高BD、CE交于点 $P$ ，若 $P D = 6 ， P B = 10$ ，则AC的长为（）

A、18 B、20 C、22 D、24

查看试题解析
4. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 46 °$ ， $∠ B A C$ 的平分线与 $A B$ 的垂直平分线 $O D$ 交于点O，点E在 $B C$ 上，点F在 $A C$ 上，连接 $E F$ ，将 $∠ C$ 沿 $E F$ 折叠，点C与点 $O$ 恰好重合时，则 $∠ O E C$ 的度数（）

A、90° B、92° C、95° D、98°

查看试题解析
5. 如图，在正方形ABCD中，E、F分别是BC、CD上的点，若△AEF是边长为2的等边三角形，则正方形的边长是（）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ +1 C、 $\sqrt{3} + \sqrt{6}$ D、 $\frac{\sqrt{6} + \sqrt{2}}{2}$

查看试题解析
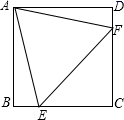6. 四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角，AM=2 $\sqrt{3}$ EF，则正方形ABCD的面积为（）

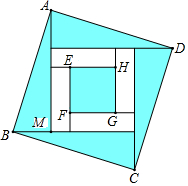A、14S B、13S C、12S D、11S

查看试题解析
7. 如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（）

A、128° B、118° C、108° D、98°

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ B = 30 °$ ， $∠ C = 50 °$ ，请观察尺规作图的痕迹（ $D$ ， $E$ ， $F$ 分别是连线与 $△ A B C$ 边的交点），则 $∠ D A E$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
9. 如图，在 $△ A B C$ 中，以点B为圆心，适当的长度为半径画弧分别交 $B A 、 B C$ 边于点P、Q，再分别以点P、Q为圆心，以大于 $\frac{1}{2} P Q$ 为半径画弧，两弧交于点M，连接 $B M$ 交 $A C$ 于点E，过点E作 $E D ∥ B C$ 交AB于点D，若 $A B = 5$ ， $A E = 3$ ，则 $△ A D E$ 的周长为（）

A、8 B、11 C、10 D、13

查看试题解析
10. 如图，点A、B、C在一条直线上，△ABD和△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④PQ∥AC．其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. 在△ABC中，AB＝AC，AB的垂直平分线与AC所在的直线相交所得的锐角为46°，则底角∠B的大小为．

查看试题解析
12. 下列三个命题：①对顶角相等；②两直线平行，内错角相等；③相等的两个实数的平方也相等.它们的逆命题成立的有.（填序号）

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A B C = 60 °$ ，点 $D$ 是 $△ A B C$ 外一点，若 $C D = 3$ ， $B D = 5 \sqrt{2}$ ． $∠ B D C = 75 °$ ，则线段 $A D$ 的长为．

查看试题解析
14. 如图，在△ABC中，AB=AC=10，BC=12，点D是边BC的中点，直线MN是AB的垂直平分线，点E是MN上的一个动点，则△BDE周长的最小值是．

查看试题解析
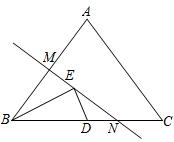15. 如图，点P是∠AOB的角平分线OC上一点，PN⊥OB于点N，点M是线段ON上一点.已知OM＝3，ON＝5，点D为OA上一点，若满足PD＝PM，则OD的长度为.

查看试题解析

三、解答题(本题共7小题，其中第16题5分，第17题7分，第18题8分，第19题8分，第20题8分，第21题9分，第22题10分，共55分)

16. 如图， $△ A B C$ 中， $∠ A C B = 90 ° ， A B = 10 ， B C = 6$ ，若点 $P$ 从点 $A$ 出发，以每秒1个单位长度的速度沿折线 $A - C - B - A$ 运动，设运动时间为 $t$ 秒 $(t > 0)$ .

(1)、若点 $P$ 在 $A C$ 上，且满足 $P A = P B$ 时，求此时 $t$ 的值；

(2)、若点 $P$ 恰好在 $∠ B A C$ 的平分线上，求 $t$ 的值.

查看试题解析
17. 在 $△ A B C$ 中， $A B = A C$ ， $B D$ 是 $△ A B C$ 的角平分线

(1)、如图1，当 $∠ A = 36 °$ 时，求证： $A D = B C$ ；

(2)、如图2，若 $∠ A = 90 °$ ，且 $A B = 1$ ，求 $A D$ 的长；

(3)、如图3，当 $∠ A = 100 °$ 时，求证： $A D + B D = B C$ .

查看试题解析
18. 如图1，在平面直角坐标系 $x O y$ 中，直线 $y = \frac{4}{3} x + 8$ 分别与x轴、y轴相交于点A、B ， $O C$ 是 $∠ A O B$ 的角平分线，交直线 $A B$ 于点C ．

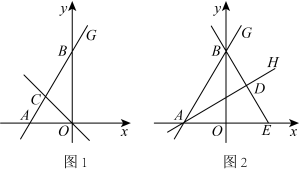(1)、求点C的坐标；

(2)、如图2， $A H$ 是 $∠ B A O$ 的角平分线，过点B作 $A H$ 的垂线交 $A H$ 于点D ，交x轴于点E求直线 $B D$ 的解析式；

(3)、在x轴上寻找点F使得 $△ A B F$ 为等腰三角形，请直接写出点F的坐标．

查看试题解析
19. $△ A B C$ 是边长为2的等边三角形，点P是直线 $B C$ 上的一点（不与B、C重合），以 $A P$ 为边向右侧作等边 $△ A P Q$ ，连接 $C Q$ ．

(1)、如图1，点P在边 $B C$ 上．
①请说明： $△ A B P ≌ △ A C Q$ ；
②求出 $△ C P Q$ 周长的最小值；

(2)、当点P在点B的左侧时，在图2中画出符合题意的图形，并直接写出 $C P 、 C Q 、 A C$ 之间的数量关系；

(3)、直接写出当 $△ C P Q$ 为直角三角形时， $B P$ 的长．

查看试题解析
20.

(1)、阅读理解
由两个顶角相等且有公共顶角顶点的特殊多边形组成的图形，如果把它们的底角顶点连接起来，则在相对位置变化的过程中，始终存在一对全等三角形，我们把这种模型称为“手拉手模型”．在如图①所示的“手拉手”图形中，小白发现若 $∠ B A C = ∠ D A E$ ， $A B = A C$ ， $A D = A E$ ，则 $△ A B D ≌ △ A C E$ ，请证明他的发现；

(2)、问题解决
如图②， $∠ B A C = ∠ D A E = 90 ° ， A B = A C ， A D = A E$ ，试探索线段 $C D ， B D ， D E$ 之间满足的等量关系，并证明；

(3)、拓展探究
如图③， $△ A B C$ 和 $△ D E C$ 是拥有公共顶点C的两个等边三角形，M点、N点、F点分别是 $D E 、 A B 、 A E$ 的中点．当 $A D = 10$ 时，请直接写出 $M N$ 的长．

查看试题解析

21. 综合与实践：

已知，等腰三角形纸片ABC中，AB＝AC，∠BAC＝36°．现要将其剪成三张小纸片，使每张小纸片都是等腰三角形（不能有剩余）．下面是小文借助尺规解决这一问题的过程，请阅读后完成相应任务．

作法：如图1所示，

①分别作AB，AC的垂直平分线，交于点P；

②连接PA，PB，PC．

结论：沿线段PA，PB，PC剪开，即可得到三个等腰三角形，

理由：∵点P在线段AB的垂直平分线上，

∴…….. （依据）．

同理，PA＝PC．

∴PA＝PB＝PC．

∴△PAB、△PBC、△PAC都是等腰三角形

任务：

(1)、上述过程中，横线上的结论为，括号中的依据为．

(2)、受小文的启发，同学们想到另一种思路：如图2，以B为圆心，BC长为半径画弧，交AC于点D，交AB于点E．在此基础上构造两条线段（以图中标有字母的点为端点）作为裁剪线，也可解决问题！请在图2中画出一种裁剪方案，直接写出得到的三个等腰三角形及相应顶角的度数．

(3)、如图3，等腰三角形纸片ABC中，AB＝AC，∠BAC＝108°，请从A，B两题中任选一题作答、我选择题．

A．请在图3中设计出一种裁剪方案，将该三角形纸片分成三个等腰三角形（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）．

B．请在图3中设计出一种裁剪方案，将该三角形纸片分成四个等腰三角形，且四个三角形互不全等（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）．

查看试题解析

22. 【背景介绍】
勾股定理是几何学中的明珠，充满着魅力，千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者，向常春在1994年构造发现了一个新的证法．如图．

(1)、【小试牛刀】
把两个全等的直角三角形如图1放置，其三边长分别为 $a$ ， $b$ ， $c$ ．显然， $∠ D A B = ∠ B = 90 °$ ， $A C ⊥ D E$ ．请用 $a$ ， $b$ ， $c$ 分别表示出梯形 $A B C D$ ，四边形 $A E C D$ ， $△ E B C$ 的面积，再探究这三个图形面积之间的关系，可得到勾股定理： $S_{梯形 A B C D} =$ ， $S_{△ E B C}$ ， $S_{四边形 A E C D} =$ ，则它们满足的关系式为，经化简，可得到勾股定理．

(2)、如图2，河道上 $A$ ， $B$ 两点（看作直线上的两点）相距160米， $C$ ， $D$ 为两个菜园（看作两个点）， $A D ⊥ A B$ ， $B C ⊥ A B$ ，垂足分别为 $A$ ， $B$ ， $A D = 70$ 米， $B C = 50$ 米，现在菜农要在 $A B$ 上确定一个抽水点 $P$ ，使得抽水点 $P$ 到两个菜园 $C$ ， $D$ 的距离和最短，则该最短距离为米．

(3)、【知识迁移】
借助上面的思考过程，画图说明并求代数式 $\sqrt{x^{2} + 9} + \sqrt{(12 - x)^{2} + 36}$ 的最小值 $(0 < x < 12)$ ．

查看试题解析

【培优卷】2024年北师大版数学八（下）第一章 三角形的证明 章末检测

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

二、填空题（本大题共5小题，每小题3分，共15分）

三、解答题(本题共7小题，其中第16题5分，第17题7分，第18题8分，第19题8分，第20题8分，第21题9分，第22题10分，共55分)

【培优卷】2024年北师大版数学八（下）第一章三角形的证明章末检测