【基础卷】北师大版数学八(下)第一章 三角形的证明 章末检测
试卷更新日期:2024-02-19 类型:单元试卷
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )A、70° B、20° C、70°或20° D、40°或140°2. 满足下列条件的三角形是等边三角形的个数是( )
①有两个角是60°的三角形;②有两个外角相等的等腰三角形:③三个外角(每个顶点处取一个外角)都相等的三角形;④一边上的高也是这边中线的等腰三角形.
A、1个 B、2个 C、3个 D、4个3. 如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( ) A、等边对等角 B、垂线段最短 C、等腰三角形“三线合一” D、线段垂直平分线上的点到这条线段两端点的距离相等4. 在中, , , 的对边分别是a , b , c , 下列条件中,不能判定是直角三角形的是( )A、 B、 C、 D、 , ,5. 以下列长度的线段不能围成直角三角形的是( )A、5,12, 13 B、 C、 ,3,4 D、2,3,46. 如图, , , 表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在( )
A、等边对等角 B、垂线段最短 C、等腰三角形“三线合一” D、线段垂直平分线上的点到这条线段两端点的距离相等4. 在中, , , 的对边分别是a , b , c , 下列条件中,不能判定是直角三角形的是( )A、 B、 C、 D、 , ,5. 以下列长度的线段不能围成直角三角形的是( )A、5,12, 13 B、 C、 ,3,4 D、2,3,46. 如图, , , 表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在( )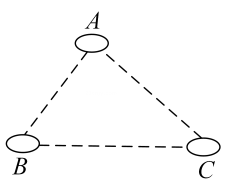 A、 , 两边高线的交点处 B、 , 两边中线的交点处 C、 , 两边垂直平分线的交点处 D、 , 两内角平分线的交点处7. 如图,为线段的垂直平分线上一点,若 , 则的长为( )
A、 , 两边高线的交点处 B、 , 两边中线的交点处 C、 , 两边垂直平分线的交点处 D、 , 两内角平分线的交点处7. 如图,为线段的垂直平分线上一点,若 , 则的长为( )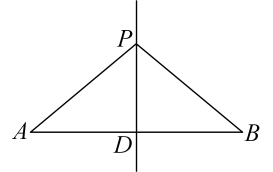 A、 B、 C、 D、8. 如图,在中, , 平分 , , , 那么点到直线的距离是( )
A、 B、 C、 D、8. 如图,在中, , 平分 , , , 那么点到直线的距离是( ) A、 B、 C、 D、9. 如图,在中, , , 平分交于点D, , 垂足为E,且 , 则的周长为( )
A、 B、 C、 D、9. 如图,在中, , , 平分交于点D, , 垂足为E,且 , 则的周长为( ) A、 B、 C、 D、10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为13,则小正方形的面积为( )
A、 B、 C、 D、10. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为13,则小正方形的面积为( )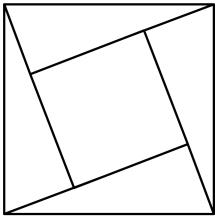 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题(本大题共5小题,每小题3分,共15分)
-
11. 面积为48的等腰三角形底边上的高为6,则腰长为 .12. 要用反证法证明等腰三角形的底角必为锐角,应先假设 .13. 命题“有两个角互余的三角形是直角三角形”的逆命题是 .14. 如图,在中, , 平分 , 垂直平分 , 若的面积等于4,则的面积为.
 15. 如图,平分 , 于点 , 点在射线上,且 . 若 , , , 则的长为 .
15. 如图,平分 , 于点 , 点在射线上,且 . 若 , , , 则的长为 .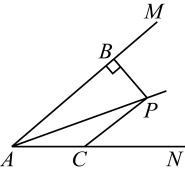
三、解答题(本题共7小题,其中第16题5分,第17题7分,第18题8分,第19题8分,第20题8分,第21题9分,第22题10分,共55分)
-
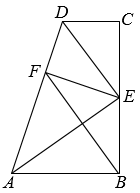
16. 如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连接QD,在新图形中,你发现了什么?请写出一条.
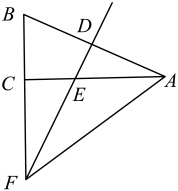
 17. 用反证法证明:一个三角形中不能有两个直角。18. 如图,与相交于点O, , , . 说明成立的理由.
17. 用反证法证明:一个三角形中不能有两个直角。18. 如图,与相交于点O, , , . 说明成立的理由. 19. 勾股定理的证明方法是多样的,其中“面积法”是常用的方法.小丽发现:当四个全等的直角三角形如图摆放时,可以用“面积法”来证明勾股定理.请写出勾股定理的内容,并利用给定的图形进行证明.
19. 勾股定理的证明方法是多样的,其中“面积法”是常用的方法.小丽发现:当四个全等的直角三角形如图摆放时,可以用“面积法”来证明勾股定理.请写出勾股定理的内容,并利用给定的图形进行证明.