【提升卷】2024年北师大版数学八(下)1.4角平分线 同步练习
试卷更新日期:2024-02-19 类型:同步测试
一、选择题
-
1. 如图,平分 , , , , , 则的长为( )
 A、13 B、12 C、11 D、102. 如图,点P是内部的一点,点P到三边的距离 , , 则的度数为( )
A、13 B、12 C、11 D、102. 如图,点P是内部的一点,点P到三边的距离 , , 则的度数为( ) A、65° B、80° C、100° D、70°3. 如图,在中, , 按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA,BC于M,N两点;②分别以点M,N为圆心,以大于的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于点D.若 , , 则线段CD的长为( )
A、65° B、80° C、100° D、70°3. 如图,在中, , 按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA,BC于M,N两点;②分别以点M,N为圆心,以大于的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于点D.若 , , 则线段CD的长为( ) A、3 B、 C、 D、4. 如图,在中, , , , 将折叠,使边落在边上,展开后得到折痕 , 则的长度为( )
A、3 B、 C、 D、4. 如图,在中, , , , 将折叠,使边落在边上,展开后得到折痕 , 则的长度为( ) A、2 B、 C、 D、5. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于 MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
A、2 B、 C、 D、5. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于 MN长为半径画弧,两弧交于点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( ) A、8 B、7 C、6 D、56. 如图,在Rt中,是的平分线,若 , 则:为( )
A、8 B、7 C、6 D、56. 如图,在Rt中,是的平分线,若 , 则:为( ) A、5:13 B、12:13 C、12:5 D、13:57. 如图,在中, , , , 以顶点A为圆心,适当长为半径画弧,分别交、于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点P,作射线交边于点D,则的值为( )
A、5:13 B、12:13 C、12:5 D、13:57. 如图,在中, , , , 以顶点A为圆心,适当长为半径画弧,分别交、于点M、N,再分别以点M、N为圆心,大于的长为半径画弧,两弧交于点P,作射线交边于点D,则的值为( )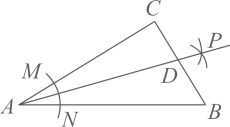 A、1 B、2.4 C、3 D、2.58. 如图,AD是的角平分线,DE⊥AC,垂足为E,交ED的延长线于点F,若DE=DF,AE=2BF.下列四个结论:①BC平分∠ABF;②;③AD⊥BC;④AB=3BF.其中正确的结论有( )
A、1 B、2.4 C、3 D、2.58. 如图,AD是的角平分线,DE⊥AC,垂足为E,交ED的延长线于点F,若DE=DF,AE=2BF.下列四个结论:①BC平分∠ABF;②;③AD⊥BC;④AB=3BF.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,在中, , , 分别以点 , 为圆心,以大于长为半径作弧,两弧相交于 , 两点,作直线交于点 , 并与的平分线交于点 , 连接 , 与相交于点 , 则度.
 10. 如图,在中, , 是角平分线,若 , , 则的面积为 .
10. 如图,在中, , 是角平分线,若 , , 则的面积为 . 11. 如图,四边形是矩形,的平分线交延长线于点E,若 , 则的长为 .
11. 如图,四边形是矩形,的平分线交延长线于点E,若 , 则的长为 .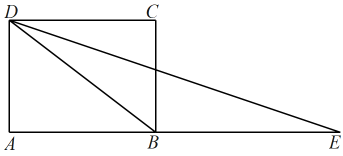 12. 如图,在四边形中,对角线平分 , , , 若点是边上一动点,则的最小值为 .
12. 如图,在四边形中,对角线平分 , , , 若点是边上一动点,则的最小值为 .
三、作图题
-
13. 如图,在△ABC中,D是AB边上一点,且BC=BD . 按下列要求完成尺规作图(保留作图痕迹,不写作法,请标明字母).

⑴作∠ABC的角平分线交CD于点E;
⑵作线段AD的垂直平分线交AD于点F;
⑶连接EF , 直接写出线段EF和AC的数量关系及位置关系.
四、综合题
-
14. 如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
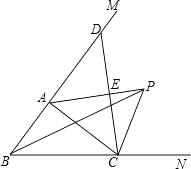 (1)、求证:PA平分∠BAC的外角∠CAM;(2)、过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.15. 如图,点A是射线OE:y=x(x≥0)上的一个动点,过点A作x轴的垂线,垂足为B,过点B作OA的平行线交∠AOB的平分线于点C
(1)、求证:PA平分∠BAC的外角∠CAM;(2)、过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.15. 如图,点A是射线OE:y=x(x≥0)上的一个动点,过点A作x轴的垂线,垂足为B,过点B作OA的平行线交∠AOB的平分线于点C (1)、若A点坐标为(2,2),求BC的长度;(2)、如图2,过点C作CG⊥AB于点G,CH⊥OE于点H,求证:AC平分∠BAE.(3)、在(1)的条件下,射线OC与AB交于点D,在第一象限内是否存在一点P使得△PCA≌△BDC?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、若A点坐标为(2,2),求BC的长度;(2)、如图2,过点C作CG⊥AB于点G,CH⊥OE于点H,求证:AC平分∠BAE.(3)、在(1)的条件下,射线OC与AB交于点D,在第一象限内是否存在一点P使得△PCA≌△BDC?若存在,请求出点P的坐标;若不存在,请说明理由.
-