【培优卷】2024年北师大版数学八(下)1.4角平分线 同步练习
试卷更新日期:2024-02-19 类型:同步测试
一、选择题
-
1. 如图,在等腰△ 中, , ,O是△ 外一点,O到三边的垂线段分别为 , , ,且 ,则 的长度为( )
 A、5 B、6 C、 D、2. 如图,在中, , , 、是的两条角平分线, , 是上的一个动点,则线段最小值的是( )
A、5 B、6 C、 D、2. 如图,在中, , , 、是的两条角平分线, , 是上的一个动点,则线段最小值的是( ) A、3 B、4 C、5 D、63. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3 , EF=3,则FN的长为( )
A、3 B、4 C、5 D、63. 由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3 , EF=3,则FN的长为( ) A、2 B、 C、 D、34. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,以点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N , 再分别以M , N为圆心,大于的长为半径画弧,两弧在∠CAB的内部相交于点P , 画射线AP与BC交于点D , DE⊥AB , 垂足为E . 则下列结论错误的是( )
A、2 B、 C、 D、34. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,以点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N , 再分别以M , N为圆心,大于的长为半径画弧,两弧在∠CAB的内部相交于点P , 画射线AP与BC交于点D , DE⊥AB , 垂足为E . 则下列结论错误的是( )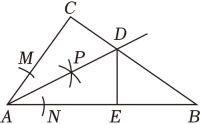 A、∠CAD=∠BAD B、CD=DE C、 D、5. 如图,在中,的垂直平分线与的外角平分线交于点D , 于点E , 交的延长线于点F , 则下列结论:①;②;③;④若 , , 则 , 其中一定成立的有( )
A、∠CAD=∠BAD B、CD=DE C、 D、5. 如图,在中,的垂直平分线与的外角平分线交于点D , 于点E , 交的延长线于点F , 则下列结论:①;②;③;④若 , , 则 , 其中一定成立的有( )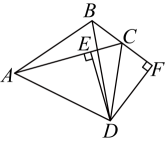 A、1个 B、2个 C、3个 D、4个6. 如图, 在△ABC中, , 的平分线与的平分线交于点 , 得 , 的平分线与的平分线交于点 , 得 , …,的平分线与的平分线交于点 , 得 , 则( )
A、1个 B、2个 C、3个 D、4个6. 如图, 在△ABC中, , 的平分线与的平分线交于点 , 得 , 的平分线与的平分线交于点 , 得 , …,的平分线与的平分线交于点 , 得 , 则( ) A、 B、 C、 D、7. 如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CEBD;②ABCD;③FQ平分∠AFP;④∠B+∠E=140°;⑤∠QFM=20°.其中结论正确的序号是( )
A、 B、 C、 D、7. 如图,点E在CA延长线上,DE,AB交于点F,且∠BDE=∠AEF,∠B=∠C,∠EFA比∠FDC的余角小10°,P为线段DC上一动点,Q为PC上一点,且满足∠FQP=∠QFP,FM为∠EFP的平分线.下列结论:①CEBD;②ABCD;③FQ平分∠AFP;④∠B+∠E=140°;⑤∠QFM=20°.其中结论正确的序号是( ) A、①②③④⑤ B、①②③④ C、②③④ D、①⑤8. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( )
A、①②③④⑤ B、①②③④ C、②③④ D、①⑤8. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
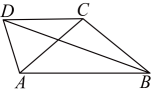
9. 如图,在四边形中,对角线平分 , , 则 .
 10. 如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB= .
10. 如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB= . 11. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号:
11. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号: 12. 如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
12. 如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1 ,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2 ,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3 , …,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En .
若∠En=1度,那∠BEC等于度。

三、作图题
-
13. 如图,Rt△ABC中,∠ACB=90°.
 (1)、尺规作图:在斜边AB上找一点D , 使AD=AC , 作∠BAC的平分线,交BC于点E , 连结DE;(不写作法,保留作图痕迹)(2)、在(1)的条件下,求证:△BDE是直角三角形.
(1)、尺规作图:在斜边AB上找一点D , 使AD=AC , 作∠BAC的平分线,交BC于点E , 连结DE;(不写作法,保留作图痕迹)(2)、在(1)的条件下,求证:△BDE是直角三角形.证明:∵AE平分∠BAC ,
∴ ▲ = ▲ ,
在△ACE和△ADE中,
,
∴△ACE≌△ADE ,
∵∠ACB=90°,
∴ ▲ =∠ACB=90°,
∴∠BDE=90°,△BDE是直角三角形.
四、解答题

