【提升卷】2024年北师大版数学八（下）1.2直角三角形同步练习

试卷更新日期：2024-02-19 类型：同步测试

进入出卷网下载

一、选择题

1. 在 $△ A B C$ 中，若 $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别是a，b，c，则下列条件中，不能判定 $△ A B C$ 是直角三角形的是（）

A、 $(a + b) (a - b) = c^{2}$ B、 $∠ C - ∠ B = ∠ A$ C、 $a = \sqrt{5}$ ， $b = \sqrt{12}$ ， $c = \sqrt{13}$ D、 $a ： b ： c = 3 ： 4 ： 5$

查看试题解析
2. 如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，则下列结论不一定成立的是（）

A、∠1+∠2=90° B、∠3=60° C、∠2=∠3 D、∠1=∠4

查看试题解析
3. 如图，将两个完全相同的 $R t △ A C B$ 和 $R t △ A^{'} C^{'} B^{'}$ 拼在一起，其中点 $A'$ 与点 $B$ 重合，点 $C'$ 在边 $A B$ 上，连接 $B' C$ ，若 $∠ A B C = ∠ A' B' C' = 30 °$ ， $A C = A' C' = 2$ ，则 $B' C$ 的长为（　　）

A、 $2 \sqrt{7}$ B、 $4 \sqrt{7}$ C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
4. 下面几组数：①7，8，9；②12，9，15；③m²＋n² ， m²－n² ， 2mn(m，n均为正整数，m>n)；④a² ， a²＋1，a²＋2.其中能组成直角三角形的三边长的是( )

A、①② B、②③ C、①③ D、③④

查看试题解析
5. 如图， $B E = C F$ ， $A E ⊥ B C$ 于点E ， $D F ⊥ B C$ 于点F ，要根据“HL”证明 $Rt △ A B E ≌ Rt △ D C F$ ，则还需要添加一个条件是（）

A、 $A E = D F$ B、 $∠ A = ∠ D$ C、 $A B = D C$ D、 $∠ B = ∠ C$

查看试题解析
6. 如图，在平面直角坐标系 $x o y$ 中， $P (4 ， 4)$ ， A、B分别是x轴正半轴、y轴正半轴上的动点，且 $△ A B O$ 的周长是8，则P到直线 $A B$ 的距离是（）

A、4 B、3 C、2.5 D、2

查看试题解析
7. 我国是最早了解勾股定理的国家之一，在《周髀算经》中记载了勾股定理的公式与证明，相传是由商高发现，故又称之为“商高定理”．下列四幅图中，不能证明勾股定理的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，已知直角三角形的直角边分别为a、b，斜边为c，以直角三角形的三边为边（或直径），分别向外作等边三角形、半圆、等腰直角三角形和正方形．那么，这四个图形中，直角三角形外，其他几个图形面积分别记作 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ．
结论Ⅰ： $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 满足 $S_{1} + S_{2} = S_{3}$ 只有（4）；
结论Ⅱ：∵ $a + b > c$ ， ∴ $S_{1} + S_{2} > S_{3}$ 的有（1）（2）（3）．
对于结论Ⅰ和Ⅱ，判断正确的是（）．

A、Ⅰ对Ⅱ不对 B、Ⅰ不对Ⅱ对 C、Ⅰ和Ⅱ都对 D、Ⅰ和Ⅱ都不对

查看试题解析

二、填空题

9. 命题“如果 $m = n$ ，那么 $\sqrt{m^{2}} = \sqrt{n^{2}}$ ”的逆命题是假命题，用一组 $m$ ， $n$ 的值说明你的判断，这组 $m$ ， $n$ 的值可以是 $m =$ ， $n =$ ．

查看试题解析
10. “赵爽弦图”是我国古代数学的骄傲，它巧妙利用面积关系证明了勾股定理，如图所示的“弦图”，是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较短直角边长为a ，较长直角边长为b ，若大正方形的面积为17，每个直角三角形面积为4，那么 ${(a - b)}^{2}$ 为．

查看试题解析
11. 如图，直角 $△ A B C$ 中， $A C = 7$ ， $A B = 25$ ，则内部五个小直角三角形的周长和为．

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， A D$ 是 $∠ B A C$ 角平分线， $D E ⊥ A B$ 于点E ， $A C = 6 ， B C = 8$ ，则 $D B$ 的值为．

查看试题解析

三、综合题

13. 已知：如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点 $D ， E$ 为 $A C$ 上一点，且 $B F = A C ， D F = D C$ ．

(1)、求证： $△ B D F ≅ △ A D C$ ；

(2)、已知 $A C = 10 \sqrt{3} ， D F = 6 \sqrt{3}$ ，求 $A F$ 的长．

查看试题解析
14. 按要求作图：下面三幅网格图中的小正方形的边长都为1，每个小正方形的顶点称为格点．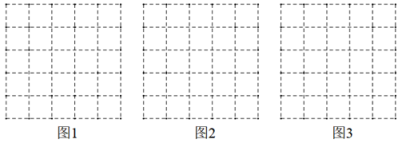

(1)、在图1中作一个边长都为整数的格点直角三角形 $A B C$ ；

(2)、在图2中作一个边长分别为 $\sqrt{2}$ ， $2 \sqrt{2}$ ， $\sqrt{10}$ 的格点三角形 $D E F$ ；

(3)、在图3中作一个有一边长为 $\sqrt{5}$ 的格点平行四边形 $G H M N$ ．

(4)、请判断图2中所作 $△ D E F$ 的形状，并说明理由．

查看试题解析
15. 如图 $1$ ，在正方形网格中，每个小正方形的边长均为 $1$ ， $△ A B C$ 的三个顶点都在格点上 $.$ 请判断 $△ A B C$ 的形状，并说明理由．

甲、乙两位同学运用所学知识，都说明了 $△ A B C$ 是直角三角形 $.$ 请你根据甲、乙两位同学的思路，补全解答过程．

甲同学说：“学习了 $《$ 勾股定理 $》$ ，已知三角形的三边，可根据勾股定理逆定理判断三角形的形状 $.$ ”

解： $△ A B C$ 是直角三角形，理由如下：

在网格中由勾股定理可以算出： $A B = \sqrt{5}$ ， $A C = \sqrt{5}$ ， $B C = \sqrt{10}$ ，

$∵ A B^{2} + A C^{2} =$     ▲         ， $B C^{2} =$     ▲         ，

      $∴$     ▲         ．

      $∴$     ▲         $= 90 °$ ．

      $∴ △ A B C$ 是角三角形．

乙同学说：“我可以运用全等三角形的相关知识，说明 $△ A B C$ 是直角三角形 $.$ ”

解： $△ A B C$ 是直角三角形，理由如下：

如图 $2$ ，由网格可知： $C D = A E = 2$ ， $∠ C D A = ∠ A E B = 90 °$ ， $A B = A C = \sqrt{5}$ ，

在 $R t △ A D C$ 和 $R t △ B E A$ 中，

      $∵ {\begin{array}{l} A C = B A = \sqrt{5} \\ C D = A E = 2 \end{array}$

      $∴ R t △ A D C$ ≌ $R t △ B E A ($    $) .$

      $∴ ∠ C A D =$     ▲         ．

又 $∵$ 在 $R t △ A E B$ 中， $∠ A B E + ∠ B A E = 90 °$ ，

      $∴ ∠ C A D +$     ▲         $= 90 °$ ，

      $∴ ∠ C A B = 180 ° - (∠ C A D + ∠ B A E) = 90 °$ ，

      $∴ △ A B C$ 是直角三角形．

查看试题解析
16. 用四个全等的直角三角形拼成如图①所示的大正方形，中间也是一个正方形．它是美丽的弦图．其中四个直角三角形的直角边长分别为a，b（a＜b），斜边长为c．

(1)、结合图①，说明：a²+b²＝c²；

(2)、如图②，将这四个全等的直角三角形无缝隙无重叠地拼接在一起，得到图形ABCDEFGH．若该图形的周长为24，OH＝3，求该图形的面积；

(3)、如图③，将八个全等的直角三角形紧密地拼接成正方形PQMN，记正方形PQMN、正方形ABCD、正方形EFGH的面积分别为S₁、S₂、S₃ ，若S₁+S₂+S₃＝18，则S₂＝　　．

查看试题解析

【提升卷】2024年北师大版数学八（下）1.2直角三角形 同步练习

一、选择题

二、填空题

三、综合题

【提升卷】2024年北师大版数学八（下）1.2直角三角形同步练习