【培优卷】2024年北师大版数学八（下）1.2直角三角形 同步练习

试卷更新日期：2024-02-19 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 已知下列命题，其中原命题与逆命题均为真命题的有（    ）

    ①若a>b ， 则ac>bc；        ②两直线平行，内错角相等；

    ③直角三角形的两个锐角互余；        ④全等三角形的周长相等．

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 2. 已知命题甲：等角的余角相等；命题乙：若a=b ， 则a2=b2 ， 则下列判断正确的是（    ）
    A、命题甲的逆命题的题设是两个角相等 B、命题乙的逆命题的结论是a2=b2 C、命题甲的逆命题是假命题 D、命题乙的逆命题是假命题

    查看试题解析

  • 3. 在△ABC中，它的三边分别为a，b，c，下列条件：①∠A=12∠B=13∠C，②∠A=∠B-∠C，③∠A：∠B：∠C=3：4：5，④a：b：c=2：3：5其中，能确定△ABC是直角三角形的条件为（ ）
    A、②③④ B、①③④ C、①②④ D、①②③

    查看试题解析

  • 4. 如图，在正方形方格中，每个小正方形的边长都是一个单位长度，点A，B，C，D，E均在小正方形方格的顶点上，线段AB，CD交于点F.若∠CFB=α，则∠ABE等于（ ）

    A、180°-α B、180°-2a C、9o°+α D、90°+2α

    查看试题解析

  • 5. 如图，在正方形网格中，每个小正方形的边长都是1，AB、CD、EF、GH四条线段，其中能组成直角三角形三边的一组线段是（   ）

    A、AB、CD、GH B、AB、CD、EF C、AB、EF、GH D、CD、EF、GH

    查看试题解析

  • 6. 如图，在△ABC中，∠C=90° ， AD平分∠BAC交BC于点D ， DE⊥AB于点E ， 则下列结论：①AD平分∠CDE；②∠BDE=∠BAC；③DE平分∠ADB；④若AC=4BE ， 则S△ABC=8S△BDE ． 其中正确的有（　　）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 7. 如图，在△ABC中，AC=BC ， AM为△ABC的角平分线，D为AB的中点，AM与CD相交于点P ， 过点D作DE垂直AM于点E ， 过点E作EN∥AC交AB于点N ， 有下列说法：①∠1+∠2>90° ． ②∠ADE=∠EDC+∠ACD ， ③N为AD的中点，④S△BPC=S△APC ． 其中，正确的是（　　）

      

    A、①③ B、①②③ C、②③④ D、①②③④

    查看试题解析

  • 8. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形的面积为49，小正方形的面积为4.若用x，y表示直角三角形的两直角边(x>y)，则下列四个说法：①x2+y2=49，②x-y=2，③2xy+4=49，④x+y=9.其中正确的是（ ）

    A、①③④ B、②④ C、①②③ D、①②③④

    查看试题解析

二、填空题

  • 9. 在△ABC中，AB=10 ， BC=6 ， AC=8 ， 点D在线段BC上从点C向点B移动，同时，点E在线段AB上由点A向点B移动，当点D与点B重合时运动停止，已知它们的运动速度相同，连接AD ， CE ， 则AD+CE的最小值为 ．

    查看试题解析

  • 10. 定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系xOy中，矩形OABC的边OA＝3，OC＝4，点M（2，0），在边AB存在点P ， 使得△CMP为“智慧三角形”，则点P的坐标为： ．

    查看试题解析

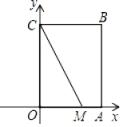  • 11. 如图，在等腰三角形ABC中，AC＝BC＝4，∠A＝30°，点D为AC的中点，点E为边AB上一个动点，连接DE，将△ADE沿直线DE折叠，点A落在点F处.当直线EF与直线AC垂直时，则AE的长为.

    查看试题解析

  • 12. 在平面直角坐标系中，一次函数 y=x+4 的图象分别与 x 轴， y 轴交于点 A ， B ，点 P 在一次函数 y=x 的图象上，则当 ΔABP 为直角三角形时，点 P 的坐标是 ．

    查看试题解析

三、解答题

  • 13. 1876年，菲尔德利用下图验证了勾股定理．

    (1)、请用含a、b、c的代数式通过两种不同的方法表示直角梯形的面积（不需要化简） ：

    方法1：

    方法2：

    (2)、利用”等面积法”。推导a、b、c之间满足的数量关系，完成勾股定理的验证．

    查看试题解析

  • 14. 在Rt△ABC中，∠ACB=90°，∠A=30°，BC=2，动点P从点A出发沿折线AC-CB向终点B运动，在AC上的速度为每秒小个单位长度，在BC上的速度为每秒1个单位长度．当点P不与点C重合时，以CP为边在点C的右上方作等边△CPQ，设点P的运动时间为t(秒)，点P到AB的距离为h．

    (1)、 AC=
    (2)、求h与1的函数关系式，并写出t的取值范围．
    (3)、当点P在AC边上运动，且点Q到AB的距离为12h时，求t的值．
    (4)、作点Q关于直线AB的对称点为Q'，当以C、P、Q'为顶点的三角形为锐角三角形时，直接写出h的取值范围．

    查看试题解析

  • 15. 阅读材料并解答问题：

    关于勾股定理的研究有一个很重要的内容是勾股数组，在数学课本中我们已经了解到，“能够成为直角三角形三条边的三个正整数称为勾股数”，以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法：

    方法1：若m为奇数（m≥3），则a=m，b= 12 （m2﹣1）和c= 12 （m2+1）是勾股数．

    方法2：若任取两个正整数m和n（m＞n），则a=m2﹣n2 ， b=2mn，c=m2+n2是勾股数．

    (1)、在以上两种方法中任选一种，证明以a，b，c为边长的△ABC是直角三角形；
    (2)、某园林管理处要在一块绿地上植树，使之构成如下图所示的图案景观，该图案由四个全等的直角三角形组成，要求每个三角形顶点处都植一棵树，各边上相邻两棵树之间的距离均为1米，如果每个三角形最短边上都植6棵树，且每个三角形的各边长之比为5：12：13，那么这四个直角三角形的边长共需植树棵．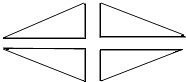

    (3)、某家俱市场现有大批如图所示的梯形边角余料(单位：cm)，实验初中数学兴趣小组决定将其加工成等腰三角形，且方案如下：

    三角形中至少有一边长为10 cm；‚三角形中至少有一边上的高为8 cm，

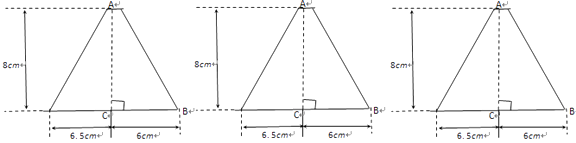
    请设计出三种面积不同的方案并在图上画出分割线，求出相应图形面积.

    查看试题解析