【提升卷】2024年北师大版数学八(下)1.1等腰三角形 同步练习
试卷更新日期:2024-02-19 类型:同步测试
一、选择题
-
1. 如图,AD是等边的中线, , 则的度数为( )
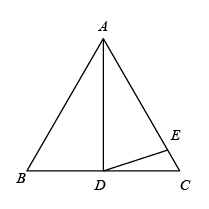 A、30° B、20° C、25° D、15°2. 如图,在△ABC 中,AB=AC,∠A=36°,BD、CE 分别是∠ABC、∠ACB 的平分线,则图中的等腰三角形有( )
A、30° B、20° C、25° D、15°2. 如图,在△ABC 中,AB=AC,∠A=36°,BD、CE 分别是∠ABC、∠ACB 的平分线,则图中的等腰三角形有( ) A、5 个 B、6 个 C、7 个 D、8 个3. 如图的网格中,点A、B在格点上,在网格上找到点C,使为等腰三角形,这样的点C共有( )
A、5 个 B、6 个 C、7 个 D、8 个3. 如图的网格中,点A、B在格点上,在网格上找到点C,使为等腰三角形,这样的点C共有( ) A、8个 B、9个 C、10个 D、11个4. 如图,在中, , , 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F,则的度数是( )
A、8个 B、9个 C、10个 D、11个4. 如图,在中, , , 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F,则的度数是( ) A、 B、 C、 D、5. 如图,是等边三角形,是边上的高,点是边的中点,点是上的一个动点,当最小时,的度数是( )
A、 B、 C、 D、5. 如图,是等边三角形,是边上的高,点是边的中点,点是上的一个动点,当最小时,的度数是( ) A、 B、 C、 D、6. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点. 若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )
A、 B、 C、 D、6. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点. 若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )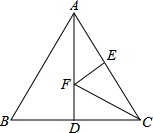 A、20° B、25° C、30° D、45°7. 已知点C在线段上,分别以、为边作等边三角形和等边三角形 , 、相交于点O,连接与相交于点N,连接与相交于点M,连接、 , 则①;②;③;④是等边三角形;⑤平分;⑥;以上结论正确的个数是( )
A、20° B、25° C、30° D、45°7. 已知点C在线段上,分别以、为边作等边三角形和等边三角形 , 、相交于点O,连接与相交于点N,连接与相交于点M,连接、 , 则①;②;③;④是等边三角形;⑤平分;⑥;以上结论正确的个数是( ) A、3个 B、4个 C、5个 D、6个8. 用反证法证明“在中,若 , 则”时,以下三个步骤正确的排列顺序是( )
A、3个 B、4个 C、5个 D、6个8. 用反证法证明“在中,若 , 则”时,以下三个步骤正确的排列顺序是( )
步骤如下:
①假设在△ABC中,∠B≥90° .
②因此假设不成立,:∴∠B<90°.
③由AB=AC,得∠B=∠C≥90°,即∠B+∠C≥180°,∴∠A+∠B+∠C> 180°,这与“三角形三个内角的和等于180°”产生矛盾.A、①③② B、①②③ C、③①② D、③②①二、填空题
-
9. 如图,已知A(4,0),B(4,4),直线y=kx+4与x轴正半轴交于点C,与y轴交于点D,将线段CD绕着点C顺时针旋转90°,点D落在点E处,连接AE,BE,若△AEB为等腰三角形,则k的值为_ .
 10. 如图,等边中,点是边的中点,的平分线交边于点 , , 点是线段上的任意一点,连接、 , 则的最小值为 .
10. 如图,等边中,点是边的中点,的平分线交边于点 , , 点是线段上的任意一点,连接、 , 则的最小值为 . 11. 如图,等边三角形的顶点 , , 则点C的坐标为;若规定把等边“先沿x轴翻折,再向左平移1个单位”为一次变换,则这样连续经过2023次变换后,等边的顶点C的坐标为 .
11. 如图,等边三角形的顶点 , , 则点C的坐标为;若规定把等边“先沿x轴翻折,再向左平移1个单位”为一次变换,则这样连续经过2023次变换后,等边的顶点C的坐标为 .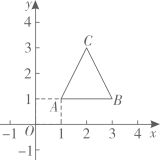 12. 如图,已知AGCF,AB⊥CF,垂足为 B,AB=BC=3 ,点 P 是射线AG 上的动点 (点 P 不与点 A 重合),点 Q是线段 CB上的动点,点 D是线段 AB的中点,连接 PD 并延长交BF于点 E,连接PQ,设AP=2t ,CQ=t,当△PQE 是以 PE为腰的等腰三角形时,t的值为.
12. 如图,已知AGCF,AB⊥CF,垂足为 B,AB=BC=3 ,点 P 是射线AG 上的动点 (点 P 不与点 A 重合),点 Q是线段 CB上的动点,点 D是线段 AB的中点,连接 PD 并延长交BF于点 E,连接PQ,设AP=2t ,CQ=t,当△PQE 是以 PE为腰的等腰三角形时,t的值为.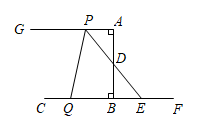
三、综合题
-
13. 如图,已知在中, , , D是上的一点, , 点P从B点出发沿射线方向以每秒2个单位的速度向右运动,设点P的运动时间为t , 连接 .
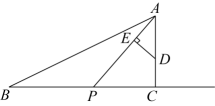 (1)、当秒时,求的长度;(2)、当△ABP为等腰三角形时,求t的值;(3)、过点D作于点E , 连接 , 在点P的运动过程中,当平分时,直接写出t的值.
(1)、当秒时,求的长度;(2)、当△ABP为等腰三角形时,求t的值;(3)、过点D作于点E , 连接 , 在点P的运动过程中,当平分时,直接写出t的值.

