【培优卷】2024年北师大版数学八（下）1.1等腰三角形同步练习

试卷更新日期：2024-02-19 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点，AD＝5，点F是AD边上的动点，则BF＋EF的最小值为（）

A、7.5 B、5 C、4 D、不能确定

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ A B C = 3 ∠ C$ ， $A D$ 为 $∠ B A C$ 的平分线， $B M ⊥ A D$ ，垂足为M，且 $A B = 6$ ， $B M = 2$ ，则 $A C =$ （）．

A、10 B、7 C、8 D、9

查看试题解析
3. △BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长，则只需知道（）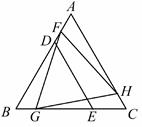

A、△ABC的周长 B、△AFH的周长 C、四边形FBGH的周长 D、四边形ADEC的周长

查看试题解析
4. 如图，△ABC为等边三角形，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，则下列四个结论：①AP平分∠BAC；②AS=AR；③QP∥AR；④△BRP≌△QSP．其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图 $1$ ， $△ A B C$ 中， $A B = A C$ ， $D$ 为 $B C$ 中点，把 $△ A B C$ 纸片沿 $A D$ 对折得到 $△ A D C$ ，如图 $2$ ，点 $E$ 和点 $F$ 分别为 $A D$ ， $A C$ 上的动点，把 $△ A D C$ 纸片沿 $E F$ 折叠，使得点 $A$ 落在 $△ A D C$ 的外部，如图 $3$ 所示．设 $∠ 1 - ∠ 2 = α$ ，则下列等式成立的是（）

A、 $∠ B A C = α$ B、 $2 ∠ B A C = α$ C、 $∠ B A C = 2 α$ D、 $3 ∠ B A C = 2 α$

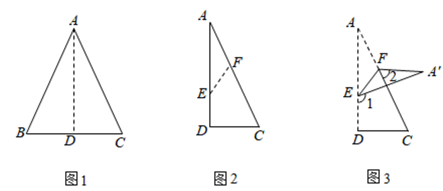查看试题解析
6.
如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线一点，当PA=CQ时，连结PQ交AC于D，则DE的长为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{2}{5}$

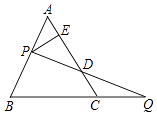查看试题解析
7. 如图，∠AOB＝30°，点M，N分别是OA，OB上的动点，P为∠AOB内一点，且OP=6，当△PMN的周长取最小值时，MN的长为（　　）

A、6 B、12 $\sqrt{3}$ -18 C、18 $\sqrt{3}$ -18 D、12

查看试题解析
8. 如图，在平面直角坐标系中，直线 $a$ 的解析式为 $y = \sqrt{3} x + 1$ ，直线 $b$ 的解析式为 $y = \frac{\sqrt{3}}{3} x$ ，直线 $a$ 交 $y$ 轴于点 $A$ ，以 $O A$ 为边作第一个等边三角形 $Δ O A B$ ，交直线 $b$ 于点 $B$ ，过点 $B$ 作 $y$ 轴的平行线交直线 $a$ 于点 $A_{1}$ ，以 $A_{1} B$ 为边作第二个等边三角形△ $A_{1} B B_{1}$ ，交直线 $b$ 于点 $B_{1}$ ， $\dots$ ，顺次这样做下去，第2020个等边三角形的边长为（）

A、 $2^{2019}$ B、 $2^{2000}$ C、4038 D、4040

查看试题解析

二、填空题

9. 已知在等腰三角形ABC中，AB=AC，∠CAB=108°，D是直线BC上一点(不与点B，C重合)，连结AD，若△ABD是等腰三角形，则∠DAC= ．

查看试题解析
10. 如图，在3×3的网格中，每个网格线的交点称为格点．已知图中A，B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有个．

查看试题解析
11. 如图，已知∠MON＝30°，点A₁ ， A₂ ， A₃ …在射线ON上，点B₁、B₂、B₃ …在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄、…均为等边三角形，若OA₁＝2，则△A₄B₄A₅的边长是．

查看试题解析
12. 如图，已知等边△ABC的边长为4，点P是边BC上一点，BP＝1，则AP＝，若点Q是边AC上一点，BQ＝AP ，则AQ＝．

查看试题解析

三、实践探究题

13. 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点.

(1)、特例感知
等腰直角三角形勾股高三角形(填“是”或“不是”)；

(2)、如图①， $△ A B C$ 为勾股高三角形，其中 $C$ 为勾股顶点， $C D$ 是 $A B$ 边上的高.若 $B D = 2 A D = 2$ ，试求线段 $C D$ 的长度.

(3)、深入探究
如图②， $△ A B C$ 为勾股高三角形，其中 $C$ 为勾股顶点且 $C A > C B$ ， $C D$ 是 $A B$ 边上的高.试探究线段 $A D$ 与 $C B$ 的数量关系，并给予证明.

(4)、推广应用
如图③，等腰三角形 $A B C$ 为勾股高三角形，其中 $A B = A C > B C$ ， $C D$ 为 $A B$ 边上的高，过点 $D$ 向 $B C$ 边引平行线与 $A C$ 边交于点 $E$ .若 $C E = a$ ，试求线段 $D E$ 的长度.

查看试题解析
14. 情境学习：

(1)、小明在预习时，涉及到一个知识点：“两个角相等的三角形是等腰三角形”，下面是两种添加辅助线的方法，选择其中一种，完成证明.
已知：如图，在 $△ A B C$ 中， $∠ B = ∠ C$ .
求证： $A B = A C$ .
方法一
证明：如图，作 $△ A B C$ 的高线AD.
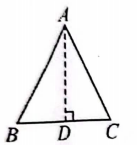
图1
方法二
证明：如图，作 $△ A B C$ 的角平分线AD.
图2

(2)、应用
如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A B C = ∠ A C B$ ， AD是BC边上的高，点E是边AB上的一动点（不与点A ， B重合），连接CE交AD于点F.作 $C G ⊥ C F$ 且 $C G = C F$ ，连接AG.
①如图3，当CE是 $∠ A C B$ 的角平分线时，求证： $A E = A F$ .
②依题意借助图4，直接写出用等式表示线段AF ， BC ， AG之间的数量关系的式子.

查看试题解析
15. 已知，在等边三角形 $A B C$ 中，点E在 $A B$ 上，点D在 $C B$ 的延长线上，且 $E D = E C$ ．

(1)、【特殊情况，探索结论】如图1，当点E为 $A B$ 的中点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你直接写出结论： $A E$ $D B$ （填“＞”、“＜”或“＝”）．

(2)、【特例启发，解答题目】如图2，当点E为 $A B$ 边上任意一点时，确定线段 $A E$ 与 $D B$ 的大小关系，请你写出结论，并说明理由． $A E$ ▲ $D B$ （填“＞”、“＜”或“＝”）；理由如下，过点E作 $E F ∥ B C$ ，交 $A C$ 于点F ．（请你完成以下解答过程）．

(3)、【拓展结论，设计新题】在等边三角形 $A B C$ 中，点E在直线 $A B$ 上，点D在线段 $C B$ 的延长线上，且 $E D = E C$ ，若 $△ A B C$ 的边长为1， $A E = 2$ ，求 $C D$ 的长（直接写出结果）．

查看试题解析

【培优卷】2024年北师大版数学八（下）1.1等腰三角形 同步练习

一、选择题

二、填空题

三、实践探究题

【培优卷】2024年北师大版数学八（下）1.1等腰三角形同步练习