新高考四大基础题(三角+数列+立体几何+概率)一天两题--专练6
试卷更新日期:2024-02-18 类型:二轮复习
一、第一天
-
1. 已知的内角的对边分别为 , , , , 的内切圆的面积为.(1)、求的值;(2)、若点在上,且三点共线,求的值.2. 已知△ABC的内角A、B、C的对边分别为a,b,c,且 ,(1)、求角A的大小:(2)、若 , 求△ABC的面积.
二、第二天
-
3. 已知数列的前n项和为(1)、求数列的通项公式;(2)、令①;②;③从上面三个条件中任选一个,求数列的前项和注:如果选择多个条件分别解答,按第一个解答计分.4. 已知为抛物线的弦,点在抛物线的准线上.当过抛物线焦点且长度为时,中点到轴的距离为.(1)、求抛物线的方程;(2)、若为直角,求证:直线过定点.
三、第三天
-
5. 在数列 , 中, , 为各项均为正数的等比数列,且其前三项和为 , 为等差数列,且其前三项和为9.(1)、求 , 的通项公式;(2)、求的前n项和.6. 已知数列和满足 , , , .(1)、求的通项公式;(2)、令 , 求数列的前项和
四、第四天
-
7. 在三棱柱中,侧面是菱形, , , .
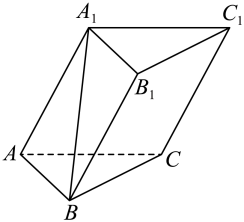 (1)、求证:;(2)、已知 , , 求直线与平面所成角的正弦值.8. 如图,在四棱锥中,底面是矩形, , , , , 点 , 分别是棱 , 的中点.
(1)、求证:;(2)、已知 , , 求直线与平面所成角的正弦值.8. 如图,在四棱锥中,底面是矩形, , , , , 点 , 分别是棱 , 的中点.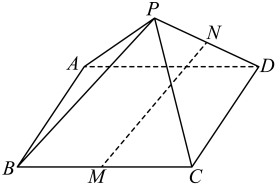 (1)、求证:平面平面;(2)、求直线与平面所成角的正弦值.
(1)、求证:平面平面;(2)、求直线与平面所成角的正弦值.五、第五天
-
9. 云计算是信息技术发展的集中体现,近年来,我国云计算市场规模持续增长.从中国信息通信研究院发布的《云计算白皮书(2022年)》可知,我国2017年至2021年云计算市场规模数据统计表如下:
年份
2017年
2018年
2019年
2020年
2021年
年份代码x
1
2
3
4
5
云计算市场规模y/亿元
692
962
1334
2091
3229
经计算得:=36.33,=112.85.
(1)、根据以上数据,建立y关于x的回归方程(为自然对数的底数).(2)、云计算为企业降低生产成本、提升产品质量提供了强大助推力.某企业未引入云计算前,单件产品尺寸与标准品尺寸的误差 , 其中m为单件产品的成本(单位:元),且=0.6827;引入云计算后,单件产品尺寸与标准品尺寸的误差.若保持单件产品的成本不变,则将会变成多少?若保持产品质量不变(即误差的概率分布不变),则单件产品的成本将会下降多少?附:对于一组数据其回归直线的斜率和截距的最小二乘估计分别为= , .
若 , 则 , ,
10. 在中,角 , , 的对边分别为 , , , 且 .(1)、求角的大小;(2)、为边上一点,且 , , , 求的长.六、第六天
-
11. 已知函数(1)、若 , 求f(x)在( , 0)上的极值;(2)、若在上恒成立,求实数a的取值范围12. 2022年“五一”期间,为推动消费市场复苏,补贴市民,深圳市各区政府发放各类消费券,其中某区政府发放了市内旅游消费券,该消费券包含 , , , , , 六个旅游项目,甲、乙、丙、丁四人每人计划从中任选两个不同的项目参加,且他们的选择互不影响.(1)、求甲、乙、丙、丁这四个人中至少有一人选择项目的概率;(2)、记为这四个人中选择项目的人数,求的分布列及数学期望;(3)、如果将甲、乙、丙、丁四个人改为个人 , 其他要求相同,问:这个人中选择项目的人数最有可能是多少人?
七、第七天
-
13. 已知函数 , .(为自然对数的底数,).(1)、若函数在区间上单调递减,求实数a的取值范围;(2)、是否存在直线l同时与的图象相切?如果存在,判断l的条数,并证明你的结论;如果不存在,说明理由.