备战2024年中考数学细点逐一突破真题训练第2章整式及其运算

试卷更新日期：2024-02-16 类型：一轮复习

进入出卷网下载

一、整式的运算

1. 下列运算正确的是（）

A、 $a (a + 1) = a^{2} + 1$ B、 $3 a^{2} + a = 3 a^{3}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a^{5} \div a^{2} = a^{3}$

查看试题解析
2. 下列运算正确的是

A、 $- (a - 1) = - a - 1$ B、 ${(- 2 a^{3})}^{2} = 4 a^{6}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{3} + a^{2} = 2 a^{5}$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $a \div b \cdot \frac{1}{b} = a$ C、 $\frac{2 a}{a - 1} - \frac{2}{a - 1} =$ 2 D、 ${(\frac{b}{a^{2}})}^{3} = \frac{b^{3}}{a^{5}}$

查看试题解析
4. 计算： $2 x \cdot (- 3 x y^{2}) =$ ．

查看试题解析
5. 已知a＝ $\frac{1}{\sqrt{5} + 2}$ ， b＝ $\frac{1}{\sqrt{5} - 2}$ ．

(1)、求a+b的值；

(2)、设m是a小数部分，n是b整数部分，求代数式4m²+4mn+n²的值．

查看试题解析
6. 下列去括号正确的是（）

A、 $3 (2 x + 3 y) = 6 x + 3 y$ B、 $- 0.5 (1 - 2 x) = - 0.5 + x$ C、 $- 2 (\frac{1}{2} x - y) = - x - 2 y$ D、 $- (2 x^{2} - x + 1) = - 2 x^{2} + x$

查看试题解析
7. 下列说法正确的是（）

A、- 2不是单项式 B、 $- a$ 表示负数 C、 $\frac{3 a b}{5}$ 的系数是3 D、 $x + \frac{a}{x} + 1$ 不是多项式

查看试题解析
8. 已知关于x，y的代数式ax²+2x+x²﹣3y²﹣bx+4y﹣5的值与x的取值无关，则a﹣b= ．

查看试题解析
9. 数学课上，老师用图1中的一张边长为a的正方形纸片A，1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C，拼成了如图2所示的大正方形，观察图形并解答下列问题：

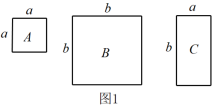
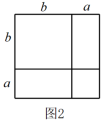
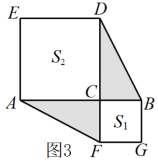(1)、由图1和图2可以得到的等式为（用含a，b的等式表示）；

(2)、莉莉想用这三种纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 的大长方形，求需A，B，C三种纸片各多少张；

(3)、如图3，S₁ ， S₂分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上， $S_{1} + S_{2} = 20$ ， $p + q = 6$ ．求图中阴影部分的面积．

查看试题解析
10. 如图，长方形ABCD被分成六个大小不一的正方形，已知中间一个小正方形的面积为4，求长方形ABCD中最大正方形与最小正方形的面积之差．

查看试题解析

二、因式分解

11. 下列各式从左到右的变形中，属于因式分解的是（）

A、 $6 x^{2} y = 2 x ∙ 3 x y$ B、 $x^{3} - 2 x y = x (x^{2} - 2 y)$ C、 $(a + 3) (a - 3) = a^{2} - 9$ D、 $x^{2} + 4 x + 1 = x (x + 4) + 1$

查看试题解析
12. 下列因式分解正确的是（）

A、 $- x^{2} + 4 x = - x (x + 4)$ B、 $x^{2} + x y + x = x (x + y)$ C、 $x^{2} - 4 x + 4 = (x + 2) (x - 2)$ D、 $x (x - y) + y (y - x) = (x - y)^{2}$

查看试题解析
13. 因式分解： $m n - 16 n =$ ．

查看试题解析
14. 分解因式：4x²﹣16= ．

查看试题解析
15. 分解因式： $a^{2} (x - y) + 9 (y - x) =$ ．

查看试题解析
16. 分解因式：a﹣6ab+9ab²= ．

查看试题解析

三、列代数式及代数式求值

17. 已知： $a - b = 2$ ，则 $a^{2} - b^{2} - 4 b - 1 =$ ．

查看试题解析
18. 若将多项式 $x^{2} - a x + b$ 因式分解为 $(x - 2) (x + 5)$ ，则 $(- 3 a + b)^{2023}$ 的值为（）

A、 $0$ B、 $- 1$ C、 $1$ D、 $1$ 或 $- 1$

查看试题解析
19. 已知 $a$ ， $b$ 都是实数，若 $| a + 1 | + {(b - 2022)}^{2} = 0$ ，则 $a^{b} =$ ．

查看试题解析

四、规律探索题

20. 如图， $△ O A_{1} B_{1}$ 、 $△ A_{1} A_{2} B_{2}$ 、 $△ A_{2} A_{3} B_{3}$ 、…、 $△ A_{n - 1} A_{n} B_{n}$ 都是斜边在x轴上的等腰直角三角形，点 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 、…、 $A_{n}$ 都在x轴上，点 $B_{1}$ 、 $B_{2}$ 、 $B_{3}$ 、…、 $B_{n}$ 都在反比例函数 $y = \frac{1}{x} (x > 0)$ 的图象上，则点 $B_{1}$ 的坐标为，点 $B_{203}$ 的坐标为．

查看试题解析
21. 杨辉，字谦光，南宋时期杭州人．在他1261年所著的《详解九章算法》一书中，记录了如图所示的三角形数表，称之为“开方作法本源”图，并说明此表引自11世纪中叶贾宪的《释锁算术》，并绘画了“古法七乘方图”．故此，杨辉三角又被称为“贾宪三角”．若用有序数对 $(m ， n)$ 表示第 $m$ 排从左到右第 $n$ 个数，如 $(3 ， 2)$ 表示正整数 $2 ， (4 ， 3)$ 表示正整数3，则 $(8 ， 3)$ 表示的正整数是．

查看试题解析
22. 按一定规律排列的单项式： $a ， \sqrt{2} a^{2} ， \sqrt{3} a^{3} ， \sqrt{4} a^{4} ， \sqrt{5} a^{5} ， ⋯$ ，第 $n$ 个单项式是（）

A、 $\sqrt{n}$ B、 $\sqrt{n - 1} a^{n - 1}$ C、 $\sqrt{n} a^{n}$ D、 $\sqrt{n} a^{n - 1}$

查看试题解析
23. 观察下列等式，第一个：2 $+ \frac{2}{3} = 2^{2} \times \frac{2}{3}$ ；第二个： $3 + \frac{3}{8} = 3^{2} \times \frac{3}{8}$ ；第三个： $4 + \frac{4}{15} = 4^{2} \times \frac{4}{15} ； ⋯ ⋯$

(1)、尝试： $5 + \frac{5}{24} =$ .

(2)、猜想：请用含 $n (n ⩾ 2$ ，且 $n$ 为整数）的代数式表示第 $(n - 1)$ 个等式.、

(3)、验证：请你运用学过的知识证明你的猜想.

查看试题解析
24. 【观察思考】

(1)、【规律发现】请用含n的式子填空：
第n个图案中“◎”的个数为.

(2)、第1个图案中“★”的个数可表示为 $\frac{1 \times 2}{2}$ ，第2个图案中“★”的个数可表示为 $\frac{2 \times 3}{2}$ ，第3个图案中“★”的个数可表示为 $\frac{3 \times 4}{2}$ ，第4个图案中“★”的个数可表示为 $\frac{4 \times 5}{2} ， ⋯ ⋯$ ，第 $n$ 个图案中“★”的个数可表示为.

(3)、【规律应用】
结合图案中“★”的排列方式及上述规律，求正整数n，使得连续的正整数之和1+2＋3＋……+n等于第n个图案中“◎”的个数的2倍.

查看试题解析

五、整式的化简与求值

25. 先化简，再求值： $[{(a - 2 b)}^{2} + (a + 2 b) (a - 2 b)] \div 2 a$ ，其中 $a = 2$ ， $b = - 2$ ．

查看试题解析
26. 有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示，化简： $| c - b | + | a - c | - | a + b |$ ．

查看试题解析