2024年北师大版数学七（下）1.6完全平方公式课后练习（提升版）

试卷更新日期：2024-02-15 类型：同步测试

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、x²＋x²＝x⁴ B、(a－b)²＝a²－b² C、(－a²)³＝－a⁶ D、3a²·2a³＝6a⁶

查看试题解析
2. 如图，两个正方形的边长分别为a，b，如果a+b=7，ab=11，那么阴影部分的面积为（）

A、24 B、16 C、9 D、8

查看试题解析
3. 如图，在正方形ABCD中，P是线段AC上任意一点，过点P分别作EF∥AD，MN∥AB．设正方形AEPM和正方形CFPN的面积之和为S₁ ，其余部分(即图中两阴影部分)的面积之和为S₂ ，则S₁与S₂的大小关系是（）

A、S₁>S₂ B、S₁≥S₂ C、S₁<S₂ D、S₁≤S₂

查看试题解析
4. 用如图所示的正方形和长方形卡片若干张，拼成一个边长为 $a + 2 b$ 的正方形，需要 $B$ 类卡片的张数为（）

A、6 B、2 C、3 D、4

查看试题解析
5. 若( $\frac{1}{3}$ m-y)²= $\frac{1}{9}$ m²+ $\frac{1}{5}$ mx+ $\frac{1}{16}$ ，则x、y的值分别为（）

A、 $- \frac{5}{6}$ ， $\frac{1}{4}$ 或 $\frac{5}{6}$ ， $- \frac{1}{4}$ B、 $- \frac{5}{6}$ ， $\frac{1}{4}$ C、 $\frac{5}{6}$ ， $- \frac{1}{4}$ D、 $\frac{5}{6}$ ， $\frac{1}{4}$

查看试题解析

二、填空题

6. 如图，边长为6的正方形ABCD中放置两个长和宽分别为a，b的长方形，若长方形的周长为 16，面积为 15.75，则图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ =.

查看试题解析
7. 已知x +y=5 ，xy=6 ，则x²+ y²=.

查看试题解析
8. 若非零实数a，b满足4a²+b²=4ab，则 $\frac{b}{a}$ 的值为．

查看试题解析
9. 已知a²+ab+b²=7，a²-ab+b²=9，则（a+b）²= ．

查看试题解析
10. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图）就是一例．这个三角形给出了（a+b）ⁿ（n=1，2，3，4，5，6）的展开式的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b）²=a²+2ab+b²展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）³=a³+3a²b+3ab²+b³展开式中各项的系数，等等．
有如下四个结论：

①（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵；

②当a=-2，b=1时，代数式a³+3a²b+3ab²+b³的值是-1；

③当代数式a⁴+4a³b+6a²b²+4ab³+b⁴的值是0时，一定是a=-1，b=1；

④（a+b）ⁿ的展开式中的各项系数之和为2n．

上述结论中，正确的有（写出序号即可）．

查看试题解析

三、综合题

11. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了(a+b)ⁿ(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律．例如，在三角形中第三行的三个数1，2， 1，恰好对应(a+b)²=a²+2ab+b²展开式中的系数；第四行的四个数1，3，3，1，恰好对应着(a+b)³=a³+3a²b+3ab²+b³展开式中的系数等等．

(1)、根据上面的规律，写出(a+b)⁵的展开式．

(2)、利用上面的规律计算：2⁵-5×2⁴+10×2³-10×2²+5×2-1．

查看试题解析
12. 用几个小的长方形、正方形拼成一个大的正方形，然后利用两种不同的方法计算这个大的正方形的面积，可以得到一个等式 $.$ 例如：计算图 $1$ 的面积，把图 $1$ 看作一个大正方形 $.$ 它的面积是 $(a + b)^{2}$ ；如果把图 $1$ 看作是由 $2$ 个长方形和 $2$ 个小正方形组成的，它的面积为 $a^{2} + 2 a b + b^{2}$ ，由此得到 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ．

(1)、如图 $2$ ，由几个面积不等的小正方形和几个小长方形拼成一个边长为 $(a + b + c)$ 的正方形，从中你能发现什么结论？该结论用等式表示为．

(2)、利用(1)中的结论解决以下问题：
已知 $a + b + c = 10$ ， $a b + a c + b c = 37$ ，求 $a^{2} + b^{2} + c^{2}$ 的值；

(3)、如图 $3$ ，正方形 $A B C D$ 边长为 $a$ ，正方形 $C E F G$ 边长为 $b$ ，点 $D$ ， $G$ ， $C$ 在同一直线上，连接 $B D$ 、 $D F$ ，若 $a - b = 5$ ， $a b = 6$ ，求图 $3$ 中阴影部分的面积．

查看试题解析
13. 【知识生成】通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．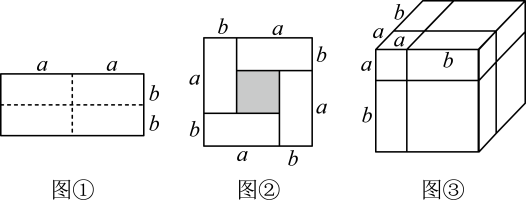
例如：如图①是一个长为 $2 a$ ，宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：

(1)、请用两种不同的方法求图②中阴影部分的面积：
方法1：；
方法2：；
由此可以得出 ${(a + b)}^{2}$ 、 ${(a - b)}^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据图③，写出一个代数恒等式：；

(3)、已知 $a + b = 3$ ， $a b = 1$ ，利用上面的规律求 $\frac{a^{3} + b^{3}}{2}$ 的值．

查看试题解析
14. 将完全平方公式作适当变形，可以用来解决很多数学问题．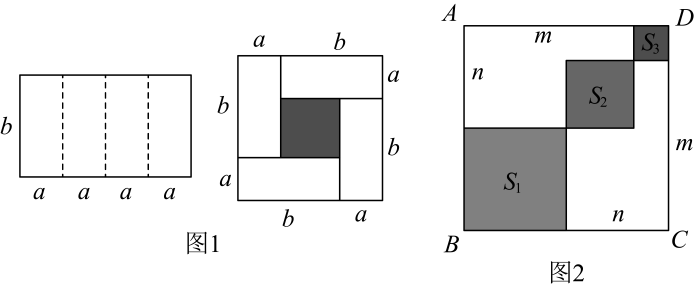

(1)、观察图1，写出代数式 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $a b$ 之间的等量关系：；

(2)、若 $x + y = 6$ ， $x y = 4$ ，则 $x^{2} + y^{2} =$ ； ${(x - y)}^{2} =$ ；

(3)、如图2，边长为5的正方形 $A B C D$ 中放置两个长和宽分别为m ， n（ $m < 5$ ， $n < 5$ ）的长方形，若长方形的周长为12，面积为 $8.5$ ，求图中阴影部分的面积 $S_{1} + S_{2} + S_{3}$ 的值．

查看试题解析
15. 将完全平方公式： $(a \pm b)^{2} = a^{2} \pm 2 a b + b^{2}$ 进行适当的变形，可以解决很多的数学问题．例如：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解：因为 $a + b = 3$ ，所以 ${(a + b)}^{2} = 9$ ，即 $a^{2} + 2 a b + b^{2} = 9$ ．
又因为 $a b = 1$ ，所以 $a^{2} + b^{2} = 7$ ．
根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 8$ ， $x^{2} + y^{2} = 40$ ，则 $x y =$ ．

(2)、拓展：若 $(4 - x)^{2} + x^{2} = 10$ ，试求 $(4 - x) x$ 的值．

(3)、应用：如图，在长方形 $A B C D$ 中， $C D = 20 ， B C = 12$ ，点E、F是BC、CD上的点，且 $B E = D F = x$ ，分别以FC、CE为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，在长方形 $A B C D$ 内侧作长方形 $C E P F$ ，若长方形 $C E P F$ 的面积为160，求图中阴影部分的面积和．

查看试题解析

2024年北师大版数学七（下）1.6完全平方公式 课后练习（提升版）

一、选择题

二、填空题

三、综合题

2024年北师大版数学七（下）1.6完全平方公式课后练习（提升版）