2024年北师大版数学七（下）1.5平方差公式课后练习（提升版）

试卷更新日期：2024-02-15 类型：同步测试

进入出卷网下载

一、选择题

1. 如图在边长为a的正方形纸片中剪去一个边长为b的小正方形，把余下的部分沿虚线剪开，拼成一个矩形，分别计算这两个图形阴影部分的面积，可以验证的等式是（）

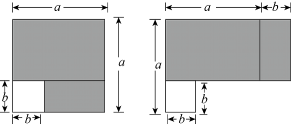A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} + a b = a (a + b)$

查看试题解析
2. 下列各式中，不能用平方差公式计算的是（）

A、(x-2y)(2y+x) B、(x-2y)(-x-2y) C、(x+2y)(-x-2y) D、(2y-x)(-x-2y)

查看试题解析
3. 观察下面图形，从图1到图2可用式子表示为（）

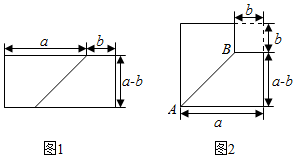A、（a+b）（a﹣b）＝a²﹣b² B、a²﹣b²＝（a+b）（a﹣b） C、（a+b）²＝a²+2ab+b² D、a²+2ab+b²＝（a+b）²

查看试题解析
4. 如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、a²﹣b²=（a+b）（a﹣b） D、无法确定

查看试题解析
5. 如图分割的正方形，拼接成长方形的方案中，可以验证（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b - b^{2}$

查看试题解析

二、填空题

6. 已知a+b=3，ab=﹣2，则a²+b²的值是．

查看试题解析
7. 已知(2a+2b-1)(2 a+2b+1)=63，则a+b的值为．

查看试题解析
8. 请你观察如图的图形，依据图形面积的关系，不需要添加辅助线，便可得到一个非常熟悉的乘法公式，这个公式是.

查看试题解析
9. 如图1，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长为20，宽为10的长方形，如图2，则图2中（1）部分的面积是．

查看试题解析
10. 已知 $a + b = 2$ ，则多项式 $a^{2} - b^{2} + 4 b + 2023$ 的值为．

查看试题解析

三、综合题

11. 如图①，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿线剪开，如图所示，拼成图②的长方形．

(1)、请你表示出图①中阴影部分的面积；
请你表示出图②中阴影部分的面；

(2)、比较两图的阴影部分面积，可以得到乘法公式：；

(3)、请应用公式计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{202 2^{2}}) (1 - \frac{1}{202 3^{2}})$ ．

查看试题解析
12. 如图1，边长为 $a$ 的大正方形中有一个边长为 $b$ 的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示）.

(1)、根据上述操作利用阴影部分的面积关系得到的等式：____（选择正确的一个）

A、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ B、 $a^{2} + a b = a (a + b)$ C、 $a^{2} - b^{2} = (a + b) (a - b)$ D、 ${(a - b)}^{2} = {(a + b)}^{2} - 4 a b$

(2)、请应用（1）中的等式，解答下列问题：
①计算： $2022 \times 2024 - 202 3^{2}$

②计算： $3 (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{64} + 1) + 1$ .

查看试题解析
13. 若x满足 $(9 - x) (x - 4) = 4$ ，求 $(4 - x)^{2} + (x - 9)^{2}$ 的值．
解：设 $9 - x = a ， x - 4 = b$ ，则 $(9 - x) (x - 4) = a b = 4 ， a + b = (9 - x) + (x - 4) = 5$

∴ ${(9 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$ ．

请仿照上面的方法求解下面问题：

(1)、若x满足 $(5 - x) (x - 2) = 2$ ，求 $(5 - x)^{2} + (x - 2)^{2}$ 的值；

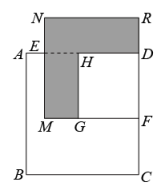(2)、若x满足 $(6 - x) (3 - x) = 1$ ，求代数式 $(9 - 2 x)^{2}$ 的值；

(3)、已知正方形ABCD的边长为x、E、F分别是AD、DC上的点，且 $A E = 3 ， C F = 5$ ，长方形EMFD的面积是48，分别以MF、DF作正方形，求阴影部分的面积．

查看试题解析
14. 聪聪和同学们用2张 $A$ 型卡片、2张 $B$ 型卡片和1张 $C$ 型卡片拼成了如图所示的长方形．其中 $A$ 型卡片是边长为 $a$ 的正方形； $B$ 型卡片是长方形； $C$ 型卡片是边长为 $b$ 的正方形．

(1)、请用含a、b的代数式分别表示出 $B$ 型卡片的长和宽；

(2)、如果 $a = 10$ ， $b = 6$ ，请求出他们用5张卡片拼出的这个长方形的面积．

查看试题解析
15. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数” $.$ 如， $4 = 2^{2} - 0^{2} ， 12 = 4^{2} - 2^{2} ， 20 = 6^{2} - 4^{2}$ ，因此4，12，20这三个数都是神秘数 $.$

(1)、28和2012这两个数是神秘数吗？为什么？

(2)、设两个连续偶数为 $2 k + 2$ 和 $2 k ($ 其中 $k$ 取非负整数 $)$ ，由这两个连续偶数构造的神秘数是4的倍数吗？为什么？

(3)、两个连续奇数的平方差 $($ 取正数 $)$ 是神秘数吗？为什么？

查看试题解析

2024年北师大版数学七（下）1.5平方差公式 课后练习（提升版）

一、选择题

二、填空题

三、综合题

2024年北师大版数学七（下）1.5平方差公式课后练习（提升版）