2024年北师大版数学七（下）1.4整式的乘法课后练习（提升版）

试卷更新日期：2024-02-15 类型：同步测试

进入出卷网下载

一、选择题

1. 已知多项式x-a与x²+2x-1的乘积中不含x²项，则常数a的值是（）

A、2 B、1 C、-2 D、-1

查看试题解析
2. 以下计算正确的是（　　）

A、（﹣2ab²）³＝8a³b⁶ B、3ab+2b＝5ab C、（﹣x²）•（﹣2x）³＝﹣8x⁵ D、2m（mn²﹣3m²）＝2m²n²﹣6m³

查看试题解析
3. 若(3x+1)(-2x+5)=-6x²+mx+n，则m的值为（）

A、3 B、-2 C、13 D、5

查看试题解析
4. 下列计算正确的是（）

A、(2x-5)(3x-7)=6x²-29x+35 B、(3x+7)(10x-8)=30x²+36x+56 C、 $(- 3 x + \frac{1}{2}) (- \frac{1}{3 x}) = 3 x^{2} + \frac{1}{2} x + \frac{1}{6}$ D、(1-x)(x+1)+(x+2)(x-2)=2x²-3

查看试题解析
5. 若p=x²y，则计算-x¹⁰y⁵(-2x²y)³的结果为（）

A、-8p⁸ B、8p⁸ C、-6p⁸ D、6p⁸

查看试题解析

二、填空题

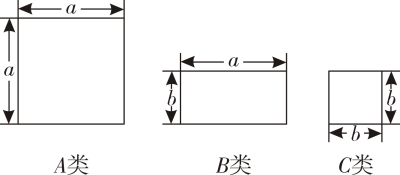
6. 如图所示的正方形和长方形卡片各有若干张，若要拼成一个长为(2a+b)，宽为(a+ b)的长方形，则需要A类卡片张，B类卡片张，C类卡片张．

查看试题解析
7. 一块三角形铁板余料的底边长是(2a+6b)米，这边上的高是(4a-5b)米，则这块铁板的面积是

查看试题解析
8. 已知A是关于x的三次多项式，B是关于x的四次多项式，则下列结论：①A+B是七次式；②A-B是一次式；③AB是七次式；④A-B是四次式，其中正确的是（填序号）.

查看试题解析
9. 若 $(x - 3) (x + a) = x^{2} + b x + 18$ ，则 $a + b =$ ．

查看试题解析
10. 要使 $(x + 3) (2 x^{2} + m x - 4)$ 的展开式中不含 $x^{2}$ 项，则m的值为．

查看试题解析

三、综合题

11.

(1)、计算：
① $(x + 9) (x + 4)$ ；
② $(x - 2) (x - 18)$ ．

(2)、分别求 $n$ 的值：
① $(x - 3) (x + m) = x^{2} + n x + 36$ ；
② $(x - 6) (x + m) = x^{2} + n x + 36$ ．

(3)、已知 $(x + p) (x + q) = x^{2} + n x + 6$ ， $p$ 、 $q$ 为正整数，求 $n$ 的值．

查看试题解析
12. 如图，某体育训练基地，有一块长 $(3 a - 5 b)$ 米，宽 $(a - b)$ 米的长方形空地，现准备在这块长方形空地上建一个长 $a$ 米，宽 $(a - 2 b)$ 米的长方形游泳池，剩余四周全部修建成休息区 $. ($ 结果需要化简 $)$

(1)、求长方形游泳池面积；

(2)、求休息区面积；

(3)、比较休息区与游泳池面积的大小关系．

查看试题解析
13.

(1)、你能求出（a-1）（ $a^{99} + a^{98} + a^{97} + \cdot \cdot \cdot + a^{2}$ +a+1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．
（a-1）（a+1）＝；
（a-1）（ $a^{2}$ +a+1）＝；
（a-1）（ $a^{3} + a^{2}$ +a+1）＝；
由此我们可以得到：（a-1）（ $a^{99} + a^{98}$ +…+a+1）＝．

(2)、利用（1）的结论，完成下面的计算：
$2^{199} + 2^{198} + 2^{197} + \cdot \cdot \cdot + 2^{2}$ +2+1．

查看试题解析
14. 如图，长为40，宽为 $x$ 的大长方形被分割为9小块，除阴影 $A$ ， $B$ 两个长方形外，其余7块是形状、大小完全相同的小长方形，其较短一边长为 $y$ ．

(1)、分别用含 $x$ ， $y$ 的代数式表示阴影 $A$ ， $B$ 两个长方形的长和宽；

(2)、分别用含 $x$ ， $y$ 的代数式表示阴影 $A$ ， $B$ 两个长方形的面积．

查看试题解析
15. 甲、乙两人共同计算一道整式： $(x + a) (2 x + b)$ ，由于甲抄错了a的符号，得到的结果是 $2 x^{2} - 7 x + 3$ ，乙漏抄了第二个多项式中x的系数，得到的结果是 $x^{2} + 2 x - 3$ ．

(1)、求 $(- 2 a + b) (a + b)$ 的值；

(2)、若整式中的a的符号不抄错，且 $a = 3$ ，请计算这道题的符合题意结果．

查看试题解析

2024年北师大版数学七（下）1.4整式的乘法 课后练习（提升版）

一、选择题

二、填空题

三、综合题

2024年北师大版数学七（下）1.4整式的乘法课后练习（提升版）