2023-2024学年广东省深圳市九年级下学期开学考模拟综合
试卷更新日期:2024-02-14 类型:开学考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )
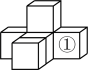 A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变2. 已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( )
A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变2. 已知某几何体的三视图(单位:cm),则这个圆锥的侧面积等于( ) A、12πcm2 B、15πcm2 C、24πcm2 D、30πcm23. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )A、k≤﹣ B、k≤﹣ 且k≠0 C、k≥﹣ D、k≥﹣ 且k≠04. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A、12πcm2 B、15πcm2 C、24πcm2 D、30πcm23. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )A、k≤﹣ B、k≤﹣ 且k≠0 C、k≥﹣ D、k≥﹣ 且k≠04. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )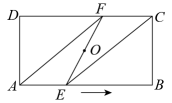 A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形5. 甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形5. 甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( ) A、从一个装有个白球和个红球的袋子中任取一球,取到红球 B、掷一枚正六面体的骰子,出现点 C、抛一枚硬币,出现正面 D、任意写一个整数,它能被整除6. 如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为l:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )
A、从一个装有个白球和个红球的袋子中任取一球,取到红球 B、掷一枚正六面体的骰子,出现点 C、抛一枚硬币,出现正面 D、任意写一个整数,它能被整除6. 如图,位似图形由三角尺与其在灯光照射下的中心投影组成,相似比为l:2,且三角尺一边长为5cm,则投影三角形的对应边长为( )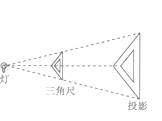
A、8cm B、20cm C、3.2cm D、10cm7. 电影《长津湖》真实生动地诠释了中国人民伟大的抗美援朝精神,一上映就受到观众的追捧,第一天票房收入2.05亿元,前三天的票房累计收入达到10.53亿元.若每天票房收入的增长率都为x,依题意可列方程( )A、2.05(1+x)=10.53 B、2.05(1+x)2=10.53 C、2.05+2.05(1+x)2=10.53 D、2.05+2.05(1+x)+2.05(1+x)2=10.538. 如图,在平行四边形中,对角线和交于点 , 下列命题是真命题的是( ) A、若 , 则平行四边形是菱形 B、若 , 则平行四边形是矩形 C、若 , 则平行四边形是矩形 D、若且 , 则平行四边形是正方形9. 如图,在中, , 下列尺规作图痕迹中,不能将的面积平分的是( )A、
A、若 , 则平行四边形是菱形 B、若 , 则平行四边形是矩形 C、若 , 则平行四边形是矩形 D、若且 , 则平行四边形是正方形9. 如图,在中, , 下列尺规作图痕迹中,不能将的面积平分的是( )A、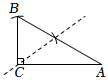 B、
B、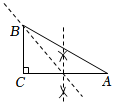 C、
C、 D、
D、 10. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
10. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )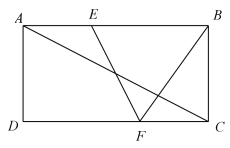 A、 B、 C、4 D、6
A、 B、 C、4 D、6二、填空题
-
11. 如果 , 那么 .12. 如图,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=.
 13. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是 .
13. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是 .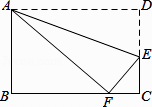 14. 平面直角坐标系 中,矩形ABOC的顶点 ,点B在x轴上,双曲线 分别交两边AC,AB于E、F两点(E、F不与A重合),沿着EF将矩形ABOC折叠使A、D两点重合.若折叠后, 是等腰三角形,则此时点D的坐标为.
14. 平面直角坐标系 中,矩形ABOC的顶点 ,点B在x轴上,双曲线 分别交两边AC,AB于E、F两点(E、F不与A重合),沿着EF将矩形ABOC折叠使A、D两点重合.若折叠后, 是等腰三角形,则此时点D的坐标为. 15. 如图,在Rt△ABC中, , , , 点M、N分别在AC、BC上,连接MN , 将△CMN沿MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN , 则MC长为
15. 如图,在Rt△ABC中, , , , 点M、N分别在AC、BC上,连接MN , 将△CMN沿MN翻折,使点C的对应点P落在AB的延长线上,若PM平分∠APN , 则MC长为
三、解答题(本题共7小题,其中第16题5分,第17题7分,第18题8分,第19题8分,第20题8分,第21题9分,第22题10分,共55分)
-
16. 解方程: (配方法)17. 图、图、图均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上,点为的中点只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
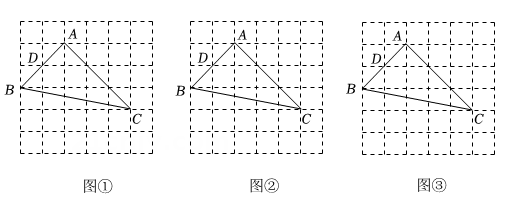 (1)、在图中的边上确定一点 , 连结 , 使 .
(1)、在图中的边上确定一点 , 连结 , 使 .
(2)、在图中的边上确定一点 , 连结 , 使 .
(3)、在图中的边上确定一点 , 连结 , 使 .18. 某商家经销一种绿茶,用于装修门而已投资3000元,已知绿茶每千克成本50元,在第一个月的试销时间内发现,销量w( )随销售单价x(元/ )的变化而变化,满足函数关系式 ,若该绿茶的月销售利润为y(元)(销售利润=单价×销售量-成本-投资)(1)、求y与x之间的函数关系式(不必写出变量x的取值范围).并求出x为何值时,y的值最大?(2)、若在第一个月里,按使y获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于90元,要想在全部收回投资的基础上使第二个月的利润达到1700元,那么第二个月里应该确定销售单价为多少元?19. 为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.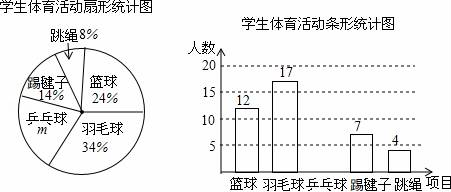 (1)、m=%,这次共抽取了名学生进行调查;并补全条形图;
(1)、m=%,这次共抽取了名学生进行调查;并补全条形图;
(2)、请你估计该校约有 名学生喜爱打篮球;
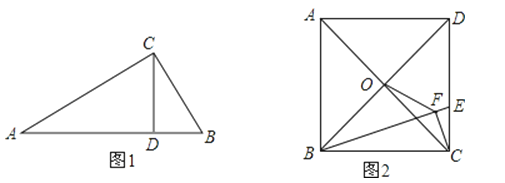
(3)、现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?20. 【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
 21. 【综合与实践】根据以下素材,探索完成任务.
21. 【综合与实践】根据以下素材,探索完成任务.素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 , 拱顶离水面 . 据调查,该河段水位在此基础上再涨达到最高.

素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂长的灯笼,如图3.为了安全,灯笼底部距离水面不小于;为了实效,相邻两盏灯笼悬挂点的水平间距均为;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
 (1)、任务1 确定桥拱形状:在图2中建立合适的直角坐标系,求抛物线的函数表达式.(2)、任务2 探究悬挂范围:在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.(3)、任务3 拟定设计方案:请你设计一种符合所有悬挂条件的方案.22.
(1)、任务1 确定桥拱形状:在图2中建立合适的直角坐标系,求抛物线的函数表达式.(2)、任务2 探究悬挂范围:在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.(3)、任务3 拟定设计方案:请你设计一种符合所有悬挂条件的方案.22.[温故知新]
在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作CF∥AD交DE的延长线于点F,再证△ADE≌△CFE,再证四边形DBCF是平行四边形,即可证明定理.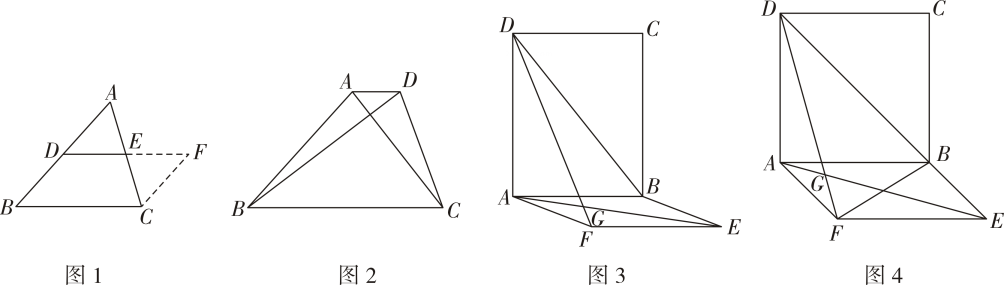 (1)、[新知体验]
(1)、[新知体验]小明思考后发现:作平行线可以构成全等三角形或平行四边形,以达到解决问题的目的.如图2,在四边形ABCD中,AD∥BC,AC⊥BD,若AC=3,BD=4,AD=1,则BC的值为
(2)、[灵活运用]如图3,在矩形ABCD和ABEF中,连接DF、AE交于点G,连接DB.若AE=DF=DB,求∠FGE的度数;
(3)、[拓展延伸]如图4在第(2)题的条件下,连接BF,若AB=4D= , 求△BEF的面积.