备考2024年高考数学冲刺专题特训：不等式

试卷更新日期：2024-02-13 类型：三轮冲刺

进入出卷网下载

一、多项选择题

1. 已知 $a ， b > 0$ ， $a + b^{2} = 1$ ，则下列选项一定正确的是（）

A、 $\sqrt{a} + b < \sqrt{2}$ B、 $b \sqrt{a}$ 的最大值为 $\frac{1}{2}$ C、 $a + 2 b$ 的最大值为2 D、 $\frac{1}{a} + \frac{4}{b^{2}} \geq 9$

查看试题解析
2. 利用“ $l n x \leq x - 1$ ”可得到许多与n（ $n \geq 2$ 且 $n \in N^{*}$ ）有关的结论，则正确的是（）

A、 $l n (n + 1) < 1 + \frac{1}{2} + \frac{1}{3} + ⋯ + \frac{1}{n}$ B、 $l n n > \frac{1}{2} + \frac{1}{3} + ⋯ + \frac{1}{n}$ C、 $(1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) ⋯ (1 + \frac{1}{2^{n}}) > e$ D、 ${(\frac{1}{n})}^{n} + {(\frac{2}{n})}^{n} + ⋯ + {(\frac{n}{n})}^{n} < \frac{e}{e - 1}$

查看试题解析
3. 古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状，把数分成许多类，如图中第一行图形中黑色小点个数：1，3，6，10，…称为三角形数，第二行图形中黑色小点个数：1，4，9，16，…称为正方形数，记三角形数构成数列 ${a_{n}}$ ，正方形数构成数列 ${b_{n}}$ ，则下列说法正确的是（）

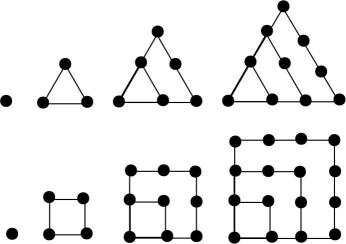A、 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + ⋯ + \frac{1}{a_{n}} = \frac{n}{n + 1}$ B、1225既是三角形数，又是正方形数 C、 $\frac{1}{b_{1}} + \frac{1}{b_{2}} + \frac{1}{b_{3}} + ⋯ + \frac{1}{b_{n}} < \frac{33}{20}$ D、 $\forall m \in N^{*} ， m \geq 2$ ，总存在 $p ， q \in N^{*}$ ，使得 $b_{m} = a_{p} + a_{q}$ 成立

查看试题解析

二、填空题

4. 在平面直角坐标系 $x O y$ 中，点 $P$ 为单位圆 $O$ 上的任一点， $M (3 ， 0)$ 、 $N (- 1 ， 1)$ ．若 $\vec{O P} = λ \vec{O M} + μ \vec{O N}$ ，则 $3 λ + μ$ 的最大值为．

查看试题解析
5. 已知函数 $f (x) = [a (x - 1) - 2 l n x] e^{x}$ 在 $(1 ， + \infty)$ 上单调递增，则实数 $a$ 的取值范围为．

查看试题解析
6. 若对任意 $x \in [1 ， 2]$ ，均有 $| x^{2} - a | + | x + a | = | x^{2} + x |$ ，则实数a的取值范围为．

查看试题解析

三、解答题

7. 已知函数 $f (x) = a e^{x} + l n (e a)$ .

(1)、当 $a = 1$ 时，求过点 $(- 2 ， 0)$ 且和曲线 $y = f (x)$ 相切的直线方程；

(2)、若对任意实数 $x > 1$ ，不等式 $f (x) ⩾ l n (x - 1)$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析
8. 已知函数 $f (x) = 2 e^{x} - a x$ ， $a \in R$ .

(1)、求函数 $f (x)$ 的单调性；

(2)、当 $a = e$ 时，求证： $f (x) > e (1 - c o s x)$ .
请考生在第22，23题中任选择一题作答，如果多做，则按所做的第一题记分.作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑.

查看试题解析
9. 设 $f (x) = \frac{x}{l n x}$

(1)、求证： $f (x) < \frac{x^{2}}{x - 1}$ ；

(2)、若 $f (x) < n l n (1 - x^{2})$ 恒成立，求整数 $n$ 的最大值．（参考数据 $l n 2 \approx 0.693$ ， $l n 3 \approx 1.099$ ）

查看试题解析
10. 已知数列 ${a_{n}}$ 是公比大于0的等比数列， $a_{1} = 4$ ， $a_{3} = 64$ .数列 ${b_{n}}$ 满足： $b_{n} = a_{2 n} + \frac{1}{a_{n}}$ （ $n ∈ N^{∗}$ ）.

(1)、求数列 ${b_{n}}$ 的通项公式；

(2)、证明： ${b_{n}^{2} - b_{2 n}}$ 是等比数列；

(3)、证明： $\sum_{n}^{k = 1} \sqrt{\frac{(2 k - 1) (2 k + 1)}{b_{k}^{2} - b_{2 k}}} < 2 \sqrt{2} (k \in N *)$ .

查看试题解析
11. 对于空间向量 $\vec{m} = (a ， b ， c)$ ，定义 $| | \vec{m} | | = m a x {| a | ， | b | ， | c |}$ ，其中 $m a x {x ， y ， z}$ 表示x ， y ， z这三个数的最大值.

(1)、已知 $\vec{a} = (3 ， - 4 ， 2)$ ， $\vec{b} = (x ， - x ， 2 x)$ .
①直接写出 $| | \vec{a} | |$ 和 $| | \vec{b} | |$ （用含 $x$ 的式子表示）；
②当 $0 \leq x \leq 4$ ，写出 $| | \vec{a} - \vec{b} | |$ 的最小值及此时 $x$ 的值；

(2)、设 $\vec{a} = (x_{1} ， y_{1} ， z_{1})$ ， $\vec{b} = (x_{2} ， y_{2} ， z_{2})$ ，求证： $| | \vec{a} + \vec{b} | | \leq | | \vec{a} | | + | | \vec{b} | |$ ；

(3)、在空间直角坐标系 $O - x y z$ 中， $A (2 ， 0 ， 0)$ ， $B (0 ， 2 ， 0)$ ， $C (0 ， 0 ， 2)$ ，点Q是 $△ A B C$ 内部的动点，直接写出 $| | \vec{O Q} | |$ 的最小值（无需解答过程）.

查看试题解析
12. 已知函数 $f (x) = l n x - (m + 1) x + \frac{1}{2} m x^{2}$ ．

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若函数 $g (x) = f (x) - \frac{1}{2} m x^{2}$ 有两个零点 $x_{1} ， x_{2}$ ，且 $x_{2} > e x_{1}$ ，求证： $x_{1} x_{2} > \frac{2}{e - 1}$ （其中 $e$ 是自然对数的底数）．

查看试题解析
13. 已知函数f（x）＝xe^x+1 ．

(1)、求f（x）过原点的切线方程；

(2)、证明：当a≤﹣2时，对任意的正实数x，都有不等式f（x）

查看试题解析
14. 已知数列 ${a_{n}}$ 中， $a_{1} = 1$ ，当 $n \geq 2$ 时，其前 $n$ 项和 $S_{n}$ 满足： $S_{n}^{2} = a_{n} (S_{n} - 1)$ ，且 $S_{n} \neq 0$ ，数列 ${b_{n}}$ 满足：对任意 $n \in N *$ 有 $\frac{b_{1}}{S_{1}} + \frac{b_{2}}{S_{2}} + ⋯ + \frac{b_{n}}{S_{n}} = (n - 1) \cdot 2^{n + 1} + 2$ .

(1)、求证：数列 ${\frac{1}{S_{n}}}$ 是等差数列；

(2)、求数列 ${b_{n}}$ 的通项公式；

(3)、设 $T_{n}$ 是数列 ${\frac{2^{n - 1}}{b_{2 n} - b_{n}}}$ 的前 $n$ 项和，求证： $T_{n} < \frac{3}{2}$ .

查看试题解析
15. 已知 $x ， y ， z \in R$ ，且 $x + 2 y + z ＝ 6$ ．

(1)、求 $x^{2} + y^{2} + z^{2}$ 的最小值；

(2)、若 $x^{2} + y^{2} + {(z - a)}^{2} \geq 1$ 成立，求 $a$ 的取值范围．

查看试题解析
16. 已知函数 $f (x) = a x e^{x} - \frac{1}{2} x^{2} - x$ ．

(1)、讨论 $f (x)$ 在 $(0 ， + ∞)$ 上的单调性；

(2)、若 $a > 0$ 时，方程 $f (x) = l n x - \frac{1}{2} x^{2}$ 有两个不等实根 $x_{1}$ ， $x_{2}$ ，求证： $x_{1} x_{2} > e^{2 - x_{1} - x_{2}}$ ．

查看试题解析
17. 数列 ${a_{n}}$ 满足： $a_{1} = 3 ， a_{n + 1} = a_{n} + 4 n + 3$ ，等比数列 ${b_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $S_{n} = c \cdot 3^{n + 1} - \frac{3}{2} \cdot n \in N^{*}$ .

(1)、求数列 ${a_{n}} ， {b_{n}}$ 的通项公式；

(2)、若数列 ${\frac{a_{n}}{n b_{n}}}$ 的前 $n$ 项和为 $T_{n}$ ，试证明 $T_{n} < 2$ .

查看试题解析
18. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，满足 $2 S_{n} = a_{n + 1} + 2 (n - 2)$ 且 $a_{1} = 4$ .

(1)、求证： ${a_{n} - 1}$ 是等比数列；

(2)、设 $b_{n} = \frac{a_{n} - 1}{a_{n} a_{n + 1}}$ ，数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求证： $T_{n} < \frac{1}{8}$ .

查看试题解析
19. 已知函数 $f (x) = | x + 2 a | + | 2 x - \frac{1}{a} | (a \neq 0)$ .

(1)、 $a = 1$ ，解不等式 $f (x) \leq 6$ ；

(2)、证明： $f (x) \geq 2$ .

查看试题解析
20. 已知 $T_{n}$ 为正项数列 ${a_{n}}$ 的前n项的乘积，且 $a_{1} = 3$ ， $T_{n}^{2} = a_{n}^{n + 1}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{a_{n} - 1}{a_{n} + 1}$ ，数列 ${b_{n}}$ 的前n项和为 $S_{n}$ ，求 $[S_{2023}]$ （ $[x]$ 表示不超过x的最大整数）．

查看试题解析
21. 已知 $f (x) = a e^{x} - a e^{- x} - 2 x$

(1)、当 $a = 1$ 时，求 $f (x)$ 单调区间；

(2)、当 $x > 0$ 时， $f (x) > 0$ 恒成立，求 $a$ 的取值范围；

(3)、设 $m > n$ ， $m ， n \in N^{*}$ ，证明： $l n \frac{m}{n} - \sum_{k = n + 1}^{m} \frac{1}{k} < \frac{m - n}{2 m n}$ ．

查看试题解析
22. 已知函数 $f (x) = | x - a | + | x - 2 |$

(1)、当 $a = 1$ 时，求不等式 $f (x) \geq 3$ 的解集；

(2)、若 $f (x) \geq 2 a - 1$ ，求 $a$ 的取值范围

查看试题解析
23. 已知 $f (x) = | 2 x + 2 | + | x - 3 |$ ．

(1)、求不等式 $f (x) \leq 5$ 的解集；

(2)、若 $f (x)$ 的最小值为 $m$ ，正实数 $a$ ， $b$ ， $c$ 满足 $a + b + c = m$ ，求证： $\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c} \geq \frac{9}{2 m}$ ．

查看试题解析
24. 已知函数 $f (x) = | 2 x | + | x - 2 a |$ ．

(1)、当 $a = 1$ 时，求不等式 $f (x) \leq 4$ 的解集；

(2)、若对任意 $x \in R$ ， $f (x) + | x - 2 a | \geq a^{2} - 5$ 恒成立，求 $a$ 的取值范围．

查看试题解析
25. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 4$ ， $S_{n} - n = \frac{1}{2} (a_{n} + 2) ， (n \in N^{*})$ ．

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ 和前 $n$ 项和 $S_{n}$ ；

(2)、设 $b_{k} = \frac{1}{(S_{2 k} + 2) S_{2 k + 1}} (k \in N^{*})$ ，数列 ${b_{n}}$ 的前 $n$ 项和记为 $T_{n}$ ，证明： $T_{n} < \frac{1}{8} ， (n \in N^{*})$

查看试题解析
26. 已知 $λ$ 为正实数，函数 $f (x) = l n (λ x + 1) - λ x + \frac{x^{2}}{2} (x > 0)$ .

(1)、若 $f (x) > 0$ 恒成立，求 $λ$ 的取值范围；

(2)、求证： $2 l n (n + 1) - \frac{5}{3} < \sum_{i = 1} (\frac{2}{i} - \frac{1}{i^{2}}) < 2 l n (n + 1)$ （ $i = 1 ， 2 ， 3 ， . . .$ ）.

查看试题解析
27. 已知等差数列 ${a_{n}}$ 满足： $a_{3} = 7$ ， $a_{2} + a_{10} = 26$ ，数列 ${a_{n}}$ 的前 $n$ 项和是 $S_{n}$ ．

(1)、求 $a_{n}$ 及 $S_{n}$ ；

(2)、令 $b_{n} = \frac{1}{a_{n} a_{n + 1}} (n \in N^{*})$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ 的取值范围．

查看试题解析
28. 已知函数 $f (x) = l n x$ ，以下证明可能用到下列结论： $x \in (0 ， 1)$ 时，① $s i n x < x < t a n x$ ；② $l n x < x - 1$ ．

(1)、 $x \in (0 ， 1)$ ，求证： $x < l n \frac{1}{1 - x}$ ；

(2)、证明： $s i n \frac{1}{2} + s i n \frac{1}{3} + ⋯ + s i n \frac{1}{n} < l n n (n \geq 2 ， n \in N)$ ．

查看试题解析
29. 已知数列 ${a_{n}}$ 中，前n项的和为 $S_{n}$ ，且 $S_{n} = 3 a_{n} - 4$

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、如果 $\frac{1}{a {}_{1}} + \frac{2}{a_{2}} + \frac{3}{a_{3}} + ⋯ + \frac{n}{a_{n}} <$ $\frac{9}{2} - 8 \times {(\frac{2}{3})}^{n}$ 恒成立，求 $n$ 最小值.

查看试题解析