备战2024年中考数学细点逐一突破真题训练第3章角、相交线与平行线
试卷更新日期:2024-02-08 类型:一轮复习
一、直线,射线,线段
-
1. 下列现象:
(1)用两个钉子就可以把木条固定在墙上;
(2)从A地到B地架设电线,总是尽可能沿着线段AB架设;
(3)植树时,只要确定两颗树的位置,就能确定同一行树所在的直线;
(4)把弯曲的公路改直,就能缩短路程.其中能用“两点之间,线段最短”来解释的现象有( )
A、(1)(2) B、(2)(3) C、(3)(4) D、(2)(4)2. 下列现象:①用两根钉子就可以把一根木条固定在墙上;②把弯曲的公路改直,就能够缩短路程;③体育课上测量某个同学的跳远成绩;④工人砌墙时,先在两端立桩拉线,然后沿着线砌墙.其中,可以用“两点确定一条直线”来解释的现象是( )A、①② B、②③ C、①④ D、③④3. 在同一平面内有四条直线,每两条直线都相交,则这四条直线的交点共有( )A、6个 B、1个或4个 C、6个或4个 D、1个或4个或6个4. 如图,已知线段AB , 点C在AB上,点P在AB外. (1)、根据要求画出图形:画直线PA , 画射线PB , 连接PC;(2)、写出图中的所有线段.5. 已知线段a,b(如图),用直尺和圆规求作:
(1)、根据要求画出图形:画直线PA , 画射线PB , 连接PC;(2)、写出图中的所有线段.5. 已知线段a,b(如图),用直尺和圆规求作: (1)、2a;(2)、2a-b.
(1)、2a;(2)、2a-b.二、角、余角、补角
-
6. 在时刻3:30,挂钟的时针与分针之间的夹角是( )A、85° B、75° C、70° D、90°7. 如果从甲船看乙船,乙船在甲船的南偏东方向,那么从乙船看甲船,甲船在乙船的( )A、北偏东 B、北偏西 C、北偏东 D、北偏西8. 已知∠α=36°14′25″,则∠α的余角的度数是 .9. 下列四个图中,能用三种方法表示同一个角的是( )A、
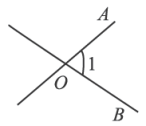 B、
B、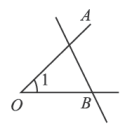 C、
C、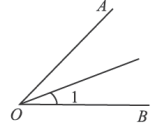 D、
D、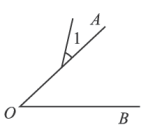 10. 学习千万条,思考第一条.请你用本学期所学知识探究以下问题:
10. 学习千万条,思考第一条.请你用本学期所学知识探究以下问题: (1)、已知点为直线上一点,将直角三角板MON的直角顶点放在点处,并在内部作射线 .
(1)、已知点为直线上一点,将直角三角板MON的直角顶点放在点处,并在内部作射线 .①如图1,三角板的一边与射线重合,且 , 若以点为观察中心,射线表示正北方向,求射线表示的方向;
②如图2,将三角板放置到如图位置,使恰好平分 , 且 , 求的度数.
(2)、已知点不在同一条直线上, , 且满足平分 , 平分 , 用含的式子表示的大小.三、相交线与角平分线
-
11. 如图,已知O为直线AB上一点,将直角三角板MON的直角顶点放在点O处,若OC是 的平分线,则下列结论正确的是( )
 A、 B、 C、 D、12. 如图,OC是的平分线,OE是的平分线, .
A、 B、 C、 D、12. 如图,OC是的平分线,OE是的平分线, .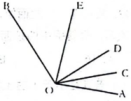 (1)、求的度数.(2)、如果 , 求的度数.13. 如图,以直线上一点为端点作射线 , 使 , 将一个直角三角板的直角顶点放在点处.(注:)
(1)、求的度数.(2)、如果 , 求的度数.13. 如图,以直线上一点为端点作射线 , 使 , 将一个直角三角板的直角顶点放在点处.(注:) (1)、如图1,若直角三角板的一边落在射线上,则;(2)、如图2,若恰好平分 , 求的度数;(3)、如图3,若始终在的内部,猜想和满足怎样的数量关系?并说明理由.14. 如图,若∠BOD=2∠AOB,OC是∠AOD的平分线,则
(1)、如图1,若直角三角板的一边落在射线上,则;(2)、如图2,若恰好平分 , 求的度数;(3)、如图3,若始终在的内部,猜想和满足怎样的数量关系?并说明理由.14. 如图,若∠BOD=2∠AOB,OC是∠AOD的平分线,则①②③④
正确的是( )
 A、①② B、③④ C、②③ D、①④
A、①② B、③④ C、②③ D、①④四、平行线判定
-
15. 如图,如果∠1=∠2,那么AB∥CD,其依据是( )
 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、同位角相等,两直线平行16. 下列命题中是真命题的是( )A、同位角相等 B、过直线外一点有且仅有一条直线与已知直线平行 C、垂直于同一直线的两直线平行 D、三角形一边的中线平分三角形的周长17. 一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 . (填序号)
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、同位角相等,两直线平行16. 下列命题中是真命题的是( )A、同位角相等 B、过直线外一点有且仅有一条直线与已知直线平行 C、垂直于同一直线的两直线平行 D、三角形一边的中线平分三角形的周长17. 一副三角板按如图所示放置,将含30°角的三角板固定,含45°角的三角板绕A点旋转,保持∠1为锐角,旋转过程中有下列结论:①∠1=∠3;②若∠2=45°,则AC∥DE.③若∠4=∠B,则AC∥DE;④若∠1=15°,则BC∥DE.其中正确的有 . (填序号) 18. 已知P是直线AB外一点,过点P作直线AB的平行线,这样的平行线( )A、有无数条 B、有且只有一条 C、不存在 D、不存在或只有一条19. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
18. 已知P是直线AB外一点,过点P作直线AB的平行线,这样的平行线( )A、有无数条 B、有且只有一条 C、不存在 D、不存在或只有一条19. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想. (1)、如图1,直线l1 , l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线l1 , l2 , l3两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、在同一平面内四条直线两两相交,最多可以形成对同旁内角.(4)、在同-平面内n条直线两两相交,最多可以形成对同旁内角.20. 木条a、b、c如图用螺丝固定在木板上,且∠ABM=50°,∠DEM=70°,将木条a、b、c看作是在同一平面内的三条直线AC、DF、MN若使直线AC、DF达到平行的位置关系,则下列描述错误的是( )
(1)、如图1,直线l1 , l2被直线l3所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线l1 , l2 , l3两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、在同一平面内四条直线两两相交,最多可以形成对同旁内角.(4)、在同-平面内n条直线两两相交,最多可以形成对同旁内角.20. 木条a、b、c如图用螺丝固定在木板上,且∠ABM=50°,∠DEM=70°,将木条a、b、c看作是在同一平面内的三条直线AC、DF、MN若使直线AC、DF达到平行的位置关系,则下列描述错误的是( ) A、木条b、c固定不动,木条a绕点B顺时针旋转20° B、木条b、c固定不动,木条a绕点B逆时针旋转160° C、木条a、c固定不动,木条b绕点E逆时针旋转20° D、木条a、c固定不动,木条b绕点E顺时针旋转110°21. 如图,下列说法正确的是( )
A、木条b、c固定不动,木条a绕点B顺时针旋转20° B、木条b、c固定不动,木条a绕点B逆时针旋转160° C、木条a、c固定不动,木条b绕点E逆时针旋转20° D、木条a、c固定不动,木条b绕点E顺时针旋转110°21. 如图,下列说法正确的是( )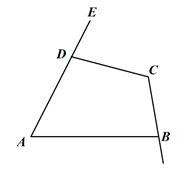 A、 与 是对顶角 B、 与 是内错角 C、 与 是同位角 D、 与 是同旁内角22. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:
A、 与 是对顶角 B、 与 是内错角 C、 与 是同位角 D、 与 是同旁内角22. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:证明:如图, ,
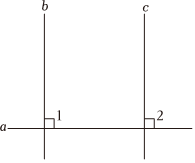
.
,
,
,
.
已知该证明过程是正确的,则证明的真命题是( )
A、在同一平面内,若 , 且 , 则 B、在同一平面内,若 , 且 , 则 C、两直线平行,同位角不相等 D、两直线平行,同位角相等五、平行线内求角度
-
23. 如图,∠AOB的一边OA为一面平面镜,∠AOB=37°36',在OB上有一点E,从点E射出一束光线,经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
 A、75°36' B、75°12' C、74°36' D、74°12'24. 如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( )
A、75°36' B、75°12' C、74°36' D、74°12'24. 如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( ) A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°25. 将一副三角尺和一张对边平行的纸条按如图所示的方式摆放,两块三角尺的一条直角边重合,含30°角的三角尺的斜边与纸条的一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是
A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°25. 将一副三角尺和一张对边平行的纸条按如图所示的方式摆放,两块三角尺的一条直角边重合,含30°角的三角尺的斜边与纸条的一边重合,含45°角的三角尺的一个顶点在纸条的另一边上,则∠1的度数是 26. 如图,AB∥DE,∠E=65°,则∠B+∠C=( )
26. 如图,AB∥DE,∠E=65°,则∠B+∠C=( ) A、135° B、115° C、36° D、65°27. 如图,若AB∥CD,则α,β,γ之间的关系为
A、135° B、115° C、36° D、65°27. 如图,若AB∥CD,则α,β,γ之间的关系为 28. 如图1所示,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥ AB,连结AE,∠B=∠E=70°。
28. 如图1所示,AB,BC被直线AC所截,D是线段AC上的点,过点D作DE∥ AB,连结AE,∠B=∠E=70°。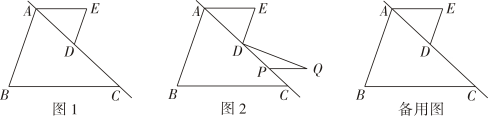 (1)、请说明AE∥BC的理由。(2)、将线段AE沿着直线AC平移得到线段PQ,连结DQ。
(1)、请说明AE∥BC的理由。(2)、将线段AE沿着直线AC平移得到线段PQ,连结DQ。①如图2所示,当DE⊥DQ时,求∠Q的度数.
②在整个运动过程中,当∠Q=2∠EDQ时,求∠Q的度数.
29. 如图 , , 点 , 分别在射线和上, . (1)、若 , 则 .(2)、嘉嘉同学发现:无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法如图 , 过点作 , 交于点 , 请你根据嘉嘉同学提供的辅助线,先确定该定值再说明理由.(3)、如图 , 把“”改为“”,其他条件保持不变,直接写出与的数量关系.30. 如图1,点A是直线上一点,C是直线上一点,B是直线之间的一点, .
(1)、若 , 则 .(2)、嘉嘉同学发现:无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法如图 , 过点作 , 交于点 , 请你根据嘉嘉同学提供的辅助线,先确定该定值再说明理由.(3)、如图 , 把“”改为“”,其他条件保持不变,直接写出与的数量关系.30. 如图1,点A是直线上一点,C是直线上一点,B是直线之间的一点, .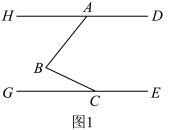 (1)、求证:;(2)、如图2,作 , 与的角平分线交于点F.若 , 求的度数;
(1)、求证:;(2)、如图2,作 , 与的角平分线交于点F.若 , 求的度数;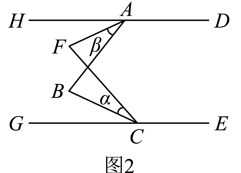 (3)、如图3,平分 , 平分 , , 已知 , 则(直接写出结果).
(3)、如图3,平分 , 平分 , , 已知 , 则(直接写出结果).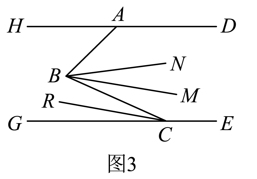
六、命题
-
31. 下列五个命题:
①如果两个数的绝对值相等,那么这两个数的平方相等;②内错角相等;③在同一平面内,垂直于同一条直线的两条直线互相平行;④两个无理数的和一定是无理数;⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是( )
A、2个 B、3个 C、4个 D、5个32. 要得知作业纸上两相交直线、所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案如图和图: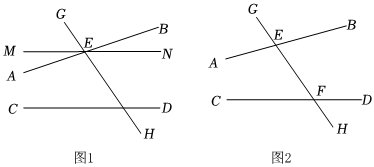
对于方案Ⅰ、Ⅱ,说法正确的是( )
方案Ⅰ:作一直线 , 交、于点 , ;
利用尺规作;
测量的大小即可.
方案Ⅱ:作一直线 , 交、于点 , ;
测量和的大小;
计算即可.
A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行33. 定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.已知:如图,直线 , 被直线所截, .
对说明理由.

方法:
如图,量角器测量所得 ,
对顶角相等 ,
角的度数相等 .
同位角相等,两直线平行 .
方法:
如图,已知 ,
对顶角相等 ,
等量代换 ,
同位角相等,两直线平行 .
下列说法正确的是( )
A、方法只要测量够组内错角进行验证,就能说明该定理的正确性 B、方法用特殊到一般的数学方法说明了该定理的正确性 C、方法用严谨的推理说明了该定理的正确性 D、方法还需说明其他位置的内错角,对该定理的说明才完整