2024年北师大版数学七年级下册期末模拟培优卷
试卷更新日期:2024-02-08 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列各式正确的是( )A、 B、 C、 D、2. 下列尺规作图不能得到平行线的是( )A、
 B、
B、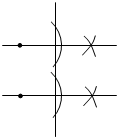 C、
C、 D、
D、 3. 如图,直线 , ,则 ( )
3. 如图,直线 , ,则 ( )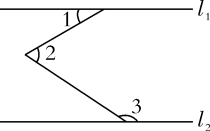 A、150° B、180° C、210° D、240°4. 已知一个函数的因变量y与自变量x的几组对应值如表,则这个函数的表达式可以是( )
A、150° B、180° C、210° D、240°4. 已知一个函数的因变量y与自变量x的几组对应值如表,则这个函数的表达式可以是( )x
…
﹣1
0
1
2
…
y
…
﹣2
0
2
4
…
A、y=2x B、y=x﹣1 C、y= D、y=x25. 如图,分别过的顶点A,B作 . 若 , , 则的度数为( ) A、 B、 C、 D、6. 如图, ,点 在 边上,已知 ,则 的度数为( )
A、 B、 C、 D、6. 如图, ,点 在 边上,已知 ,则 的度数为( ) A、 B、 C、 D、7. 如图,中, , 将逆时针旋转得到 , 交于F.当时,点D恰好落在上,此时等于( )
A、 B、 C、 D、7. 如图,中, , 将逆时针旋转得到 , 交于F.当时,点D恰好落在上,此时等于( ) A、 B、 C、 D、8. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )
A、 B、 C、 D、8. 如图所示,将一矩形纸片沿AB折叠,已知 , 则( )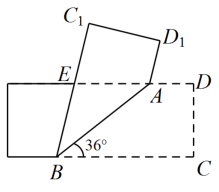 A、48° B、66° C、72° D、78°9. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )
A、48° B、66° C、72° D、78°9. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )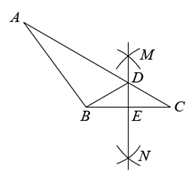 A、25 B、22 C、19 D、1810. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“烹饪”的概率为 ( )A、 B、 C、 D、
A、25 B、22 C、19 D、1810. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“烹饪”的概率为 ( )A、 B、 C、 D、二、填空题(每题3分,共18分)
-
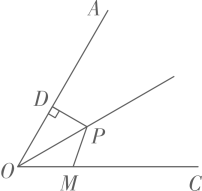
11. 若m、n满足 , 则 .12. 已知△ABC是等腰三角形.若∠A=40°,则△ABC的顶角度数是 .13. 如图,点P是 的角平分线上一点, ,垂足为点D,且 ,点M是射线 上一动点,则 的最小值为 .
 14. 如图,在和中, , , , AC与DE相交于点F.若 , 则的度数为 .
14. 如图,在和中, , , , AC与DE相交于点F.若 , 则的度数为 . 15. 如图,AB//CD,直线分别交、于点E、F,平分 , 若 , 则 .
15. 如图,AB//CD,直线分别交、于点E、F,平分 , 若 , 则 . 16. 如图,直线 ,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分 ,则 的度数为°.
16. 如图,直线 ,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分 ,则 的度数为°.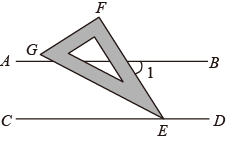
三、解答题(共7题,共72分)
-
17. 计算下列各题:(1)、计算:(15x3y+10x2y-5xy2)÷5xy.(2)、若(x-2)(x2+ax+b)的积中不含x的二次项和一次项,求ab的值.(3)、先化简,再求值:[(x-2y)2-(x-y)(x+y)-2y2]÷y,其中x=-1,y=-2.18. 佳佳和萌萌一起参加中长跑,起跑后路程与时间之间的关系如图所示.
 (1)、在上述关系中,自变量是 , 因变量是;(2)、这次比赛的路程是m;(3)、萌萌将本次中长跑分起跑、途中跑和冲刺跑三阶段,经历了两次变速,在第速度最慢,速度为;(4)、通过计算说明萌萌与佳佳何时相遇.19. 已知:如图,AB∥DE,AC∥DF,BF=EC.
(1)、在上述关系中,自变量是 , 因变量是;(2)、这次比赛的路程是m;(3)、萌萌将本次中长跑分起跑、途中跑和冲刺跑三阶段,经历了两次变速,在第速度最慢,速度为;(4)、通过计算说明萌萌与佳佳何时相遇.19. 已知:如图,AB∥DE,AC∥DF,BF=EC. (1)、求证:△ABC≌△DEF;(2)、过点C作CG⊥AB于点G,若S△ABC=9,DE=6,求CG的长.20. 某商场进行“6·18”促销活动,设计了如下两种摇奖方式:
(1)、求证:△ABC≌△DEF;(2)、过点C作CG⊥AB于点G,若S△ABC=9,DE=6,求CG的长.20. 某商场进行“6·18”促销活动,设计了如下两种摇奖方式:方式一:如图1,有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:如图2,一个均匀的转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字.转动转盘,当转盘停止后,指针指向的数字为3的倍数则获奖.
 (1)、若采用方式一,骰子掷出后,“5”朝上的概率为;(2)、若采用方式二,当转盘停止后,指针指向的数字为“5”的概率为;(3)、小明想增加获奖机会,应选择哪种摇奖方式?请通过相关计算,应用概率相关知识说明理由.21. 已知:如图①, , , 点C是上一点,且 , .
(1)、若采用方式一,骰子掷出后,“5”朝上的概率为;(2)、若采用方式二,当转盘停止后,指针指向的数字为“5”的概率为;(3)、小明想增加获奖机会,应选择哪种摇奖方式?请通过相关计算,应用概率相关知识说明理由.21. 已知:如图①, , , 点C是上一点,且 , . (1)、试判断与的位置关系,并说明理由;(2)、如图②,若把沿直线向左移动,使的顶点C与B重合,与交于点F , 此时与的位置关系怎样?请说明理由;(3)、图②中,若 , , 求四边形的面积.22. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , .
(1)、试判断与的位置关系,并说明理由;(2)、如图②,若把沿直线向左移动,使的顶点C与B重合,与交于点F , 此时与的位置关系怎样?请说明理由;(3)、图②中,若 , , 求四边形的面积.22. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , . (1)、【发现问题】
(1)、【发现问题】如图①,当 , 时,则与的数量关系是 .
(2)、【探究问题】如图②,点C , D在射线 , 上滑动,且 , 当时,与在【发现问题】中的数量关系还成立吗?说明理由.
23. 问题背景:如图①:将一副三角板中的两个直角顶点叠放在一起,其中 , , .

问题提出:
(1)、将这两个三角板按如图①放置,若 , 则;(2)、将这两个三角板按如图②放置,当时,求的度数;操作探究:
(3)、若保持两个三角板的直角顶点叠放在一起,三角板保持不动,试探究三角板如何放置时, , 此时等于多少度?请画出草图,并说明理由