2024年北师大版数学七年级下册期末模拟基础卷
试卷更新日期:2024-02-08 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列运算正确的是( )A、x2+x2=x4 B、(a-b)2=a2-b2 C、(-a2)3=-a6 D、3a2·2a3=6a62. 如图,点 E 在 BC 的延长线上,对于给出的四个条件:
①∠1=∠3;②∠2+∠5=180°;③∠4=∠B;④∠D+∠BCD=180°.
其中能判定 AD∥BC的是( )
 A、①② B、①④ C、①③ D、②④3. 如图,a,b是直尺的两边,a//b,把三角板的直角顶点放在直尺的b边上,若∠1=35°,则∠2的度数是( )
A、①② B、①④ C、①③ D、②④3. 如图,a,b是直尺的两边,a//b,把三角板的直角顶点放在直尺的b边上,若∠1=35°,则∠2的度数是( ) A、65° B、55° C、45° D、35°4. 一杯越晾越凉的水,下列能反映出水温与时间关系的图像是( )A、
A、65° B、55° C、45° D、35°4. 一杯越晾越凉的水,下列能反映出水温与时间关系的图像是( )A、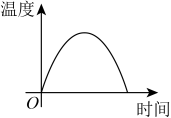 B、
B、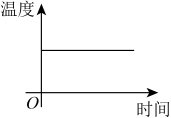 C、
C、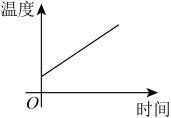 D、
D、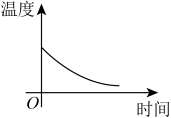 5. 如图下列各组条件中,可以判定的条件是( )
5. 如图下列各组条件中,可以判定的条件是( )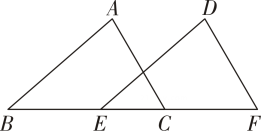 A、、、 B、、、 C、、、 D、、、、6. 如图,△ABD≌△ACE,若AB=6,AE=4,则CD的长度为( )
A、、、 B、、、 C、、、 D、、、、6. 如图,△ABD≌△ACE,若AB=6,AE=4,则CD的长度为( )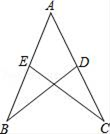 A、10 B、6 C、4 D、27. 如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( )
A、10 B、6 C、4 D、27. 如图,用直尺和圆规作已知角的平分线的示意图,则说明∠CAD=∠DAB的依据是( ) A、SAS B、ASA C、AAS D、SSS8. 下列图形中,为轴对称的图形的是( )A、
A、SAS B、ASA C、AAS D、SSS8. 下列图形中,为轴对称的图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在△ABC中,AC的垂直平分线交BC于点D , 交AC于点E , ∠B=∠ADB . 若AB=4,则DC的长是 ( ).
9. 如图,在△ABC中,AC的垂直平分线交BC于点D , 交AC于点E , ∠B=∠ADB . 若AB=4,则DC的长是 ( ).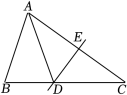 A、2 B、3 C、4 D、不能确定10. 任意抛掷一枚均匀的骰子, 结果朝上一面的点数为2的倍数的概率是( )A、 B、 C、 D、
A、2 B、3 C、4 D、不能确定10. 任意抛掷一枚均匀的骰子, 结果朝上一面的点数为2的倍数的概率是( )A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有3个黑色棋子和若干个白色棋子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑色棋子的概率是 , 则盒子中棋子的总个数是 .12. 在中, , , 点D在边上,连接 , 若为直角三角形,则的度数是.13. 若am=2,an=8,则am+n= .
14. 如图, 与 都相交, ,则 .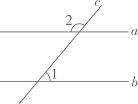 15. 如图,在中, , 分别以点B和点C为圆心,大于的长为半径作弧,两孤交于点D,作直线交于点E.若 , 则的大小为度.
15. 如图,在中, , 分别以点B和点C为圆心,大于的长为半径作弧,两孤交于点D,作直线交于点E.若 , 则的大小为度.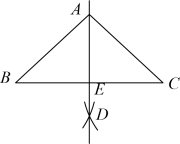 16. 如图, 和 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使 和 全等.
16. 如图, 和 中, ,在不添加任何辅助线的情况下,请你添加一个条件 , 使 和 全等.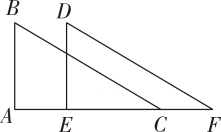
三、解答题(共8题,共72分)
-
17. 先化简再求值:其中 .18. 先化简,再求值:(x+1)(x﹣1)+x2(1﹣x)+x3 , 其中x=2
19. 如图,点E、F分别在AB、CD上,于点O, , , 求证: .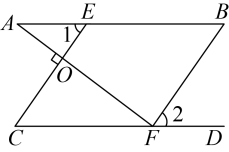
证明:∵(已知),
∴ ▲
又∵(已知),
∴ ▲ (同位角相等,两直线平行),
∴( ),
∴ ▲
又∵ ▲ (平角的定义)
∴ ▲ ,
又∵(已知),
∴( ),
∴( )
20. 今年“五一”假期期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖;指向其余数字不中奖.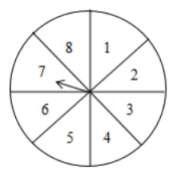 (1)、转动转盘中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、“五一”这天有1800人参与这项活动,估计获得一等奖的人数是多少?21. 如图,已知 , .
(1)、转动转盘中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、“五一”这天有1800人参与这项活动,估计获得一等奖的人数是多少?21. 如图,已知 , .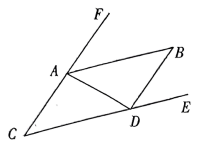 (1)、判断与所在直线是否平行,并说明理由;(2)、如果平分 , 且 , 求的度数.
(1)、判断与所在直线是否平行,并说明理由;(2)、如果平分 , 且 , 求的度数.