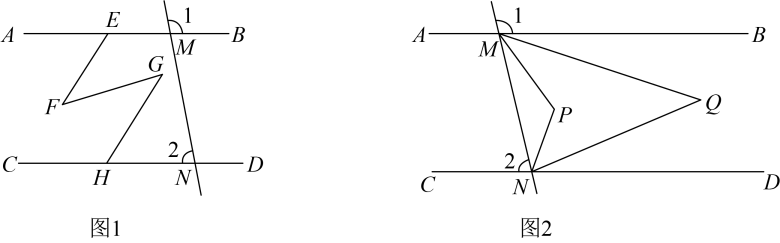2024年北师大版数学七年级下册期中模拟基础卷
试卷更新日期:2024-02-08 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 球的体积是 , 球的半径为 , 则 , 其中变量和常量分别是( )A、变量是V,R;常量是 B、变量是;常量是 C、变量是;常量是 D、变量是;常量是2. 计算的结果为( )A、 B、 C、 D、3. 如图,街道与平行,拐角 , 则拐角 ( )
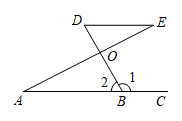
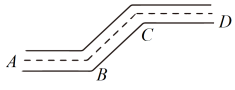 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 , 将含有角的直角三角尺按如图所示的位置放置,若 , 那么的大小为( )
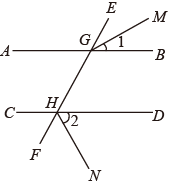
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 , 将含有角的直角三角尺按如图所示的位置放置,若 , 那么的大小为( )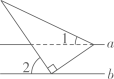 A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,直线 ,且直线a,b被直线c,d所截,则下列条件不能判定直线 的是( )
A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,直线 ,且直线a,b被直线c,d所截,则下列条件不能判定直线 的是( ) A、 B、 C、 D、8. 如图1是一个长为 , 宽为的长方形,用剪刀沿图中虚线剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
A、 B、 C、 D、8. 如图1是一个长为 , 宽为的长方形,用剪刀沿图中虚线剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( ) A、 B、 C、 D、9. 六一儿童节,爸爸妈妈带着潇潇从家出发匀速步行前往江北嘴大剧院户外广场欣赏“亲子户外江畔音乐会”,三人在途中的礼品店买了礼物后,发现音乐会即将开始.于是三人以更快的速度匀速跑步前往,最后准时到达.下面能反映潇潇离家的距离与时间的关系的大致图象是( )A、
A、 B、 C、 D、9. 六一儿童节,爸爸妈妈带着潇潇从家出发匀速步行前往江北嘴大剧院户外广场欣赏“亲子户外江畔音乐会”,三人在途中的礼品店买了礼物后,发现音乐会即将开始.于是三人以更快的速度匀速跑步前往,最后准时到达.下面能反映潇潇离家的距离与时间的关系的大致图象是( )A、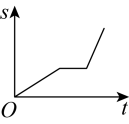 B、
B、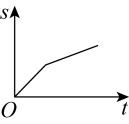 C、
C、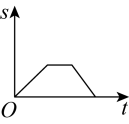 D、
D、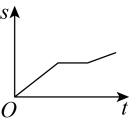 10. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )
10. 如图,l1∥l2 , ∠1=38°,∠2=46°,则∠3的度数为( )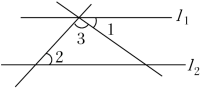 A、46° B、90° C、96° D、134°
A、46° B、90° C、96° D、134°二、填空题(每题3分,共18分)
-
11. 一个氧原子的直径为0.000000000148m,用科学记数法表示为m.12. 一辆轿车油箱中存油升,轿车行驶时平均每小时耗油升,则这辆轿车的油箱中剩余油量升与行驶时间小时之间的关系式是 .13. 如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转°
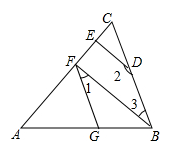
 14. 已知 , , 则的值为 .15. 若 , , 则的值为 .16. 将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则 .
14. 已知 , , 则的值为 .15. 若 , , 则的值为 .16. 将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则 .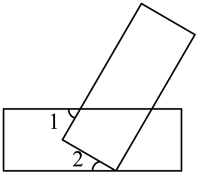
三、解答题(共9题,共72分)
-
17. 先化简,再求值:a(a+1)﹣(a﹣1)2 , 其中a= .18. 先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2 , 其中ab=﹣ .19. 定义新运算“※”:x※y=xy+x2﹣y2 , 化简(2a+3b)※(2a﹣3b),并求出当a=2,b=1时的值.20. 在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,如表是测得的弹簧的长度y与所挂物体的质量x的几组对应值:
所挂物体质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
18
20
22
24
26
28
(1)、上述表格反映了两个变量之间的关系,哪个是自变量?哪个是因变量?(2)、不挂物体时,弹簧长 cm;(3)、当所挂物体的质量为7kg时,弹簧的长度是多少?(4)、若弹簧的长度为34cm时,此时所挂重物的质量是多少?(在弹簧的允许范围内)