吉林省长春市榆树市2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-02-06 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共24分）

1. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{3}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
2. 若sinα＝ $\frac{1}{2}$ ，则锐角α＝（）

A、30° B、45° C、50° D、60°

查看试题解析
3. 一元二次方程 $x^{2} - 8 x + 20 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、只有一个实数根

查看试题解析
4. 如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上.若测得BE=20m，EC=10m，CD=20m，则河的宽度AB等于（）

A、60m B、40m C、30m D、20m

查看试题解析
5. 若点 $(3 ， a)$ 、 $(4 ， b)$ 都在二次函数 $y = {(x - 2)}^{2}$ 的图象上，则a与b的大小关系（）

A、 $a > b$ B、 $a < b$ C、 $a = b$ D、无法确定

查看试题解析
6. 如图，四边形ABCD和四边形A′B′C′D′是以点O为位似中心的位似图形，若OA：OA′＝2：3，四边形ABCD的面积等于4，则四边形A′B′C′D′的面积为（）

A、3 B、4 C、6 D、9

查看试题解析
7. 如图，河坝横断面迎水坡 $A B$ 的坡比为 $1： \sqrt{3}$ ．坝高 $B C$ 为 $4 m$ ，则 $A B$ 的长度为（）

A、 $4 \sqrt{3} m$ B、 $8 m$ C、 $8 \sqrt{3} m$ D、 $16 m$

查看试题解析
8. 如图，在 $4 \times 4$ 的正方形网格中，每个小正方形的边长均为1，已知 $∠ α$ 的顶点位于正方形网格的格点上，且 $c o s α = \frac{3 \sqrt{13}}{13}$ ，则满足条件的 $∠ α$ 是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每小题3分，共18分）

9. 计算： $\sqrt{3}$ × $\sqrt{12}$ ＝．

查看试题解析
10. 抛物线 $y = - 3 (x - 1)^{2} - 2$ 的对称轴是直线．

查看试题解析
11. 如图，一片树叶放置在 $4 \times 4$ 的正方形网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点，点 $A$ 、 $B$ 、 $C$ 均在格点上，若点 $A$ 的坐标为 $(- 1 ， 1)$ ，点 $B$ 的坐标为 $(2 ， - 1)$ ，则点 $C$ 的坐标为．

查看试题解析
12. 如图，在4×4的正方形网络中，已将部分小正方形涂上阴影，有一个小虫落到网格中，那么小虫落到阴影部分的概率是.

查看试题解析
13. 如图，学校课外生物小组的试验园地的形状是长35米、宽20米的矩形．为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为660平方米，则小道的宽为多少米？若设小道的宽为x米，则根据题意，列方程为．

查看试题解析
14. 如图，在等边三角形 $A B C$ 中， $A B = 4$ ，点 $D$ 是边 $A B$ 上一点，且 $B D = 1$ ，点 $P$ 是边 $B C$ 上一动点（ $D$ 、 $P$ 两点均不与端点重合），作 $∠ D P E = 60 °$ ， $P E$ 交边 $A C$ 于点 $E$ ．若 $C E = a$ ，当满足条件的点 $P$ 有且只有一个时，则 $a$ 的值为．

查看试题解析

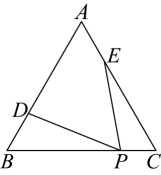
三、解答题（本大题共10小题，共78分）

15. 计算： $\sqrt{6} \times \sqrt{3} + \sqrt{24} \div \sqrt{6} - | 3 - \sqrt{2} |$ ．

查看试题解析
16. 解方程：x²﹣5x+2＝0（配方法）

查看试题解析
17. 图①、图②、图③均是4×4的正方形网格，每个小正方形的顶点称为格点，线段AB的端点均在格点上，在图②、图③中仿照图①，只用无刻度的直尺，各画出一条线段CD ，将线段AB分为2：3两部分．
要求：所画线段CD的位置不同，点C、D均在格点上

查看试题解析
18. 已知如图，抛物线的顶点D的坐标为（1，-4），且与y轴交于点C（0，-3）.

(1)、求该函数的关系式；

(2)、求该抛物线与x轴的交点A，B的坐标.

查看试题解析
19. 如图，小明为了测量学校旗杆 $C D$ 的高度，在地面离旗杆底部C处22米的A处放置高度为1.8米的测角仪 $A B$ ，测得旗杆顶端D的仰角为 $32 °$ ．求旗杆的高度 $C D$ ．（结果精确到0.1米）【参考数据： $s i n 32 ° = 0.53 ， c o s 32 ° = 0.85 ， t a n 32 ° = 0.62$ 】

查看试题解析
20. 为加快新旧动能转换，提高公司经济效益，某公司决定对近期研发出的一种电子产品进行降价促销，使生产的电子产品能够及时售出，根据市场调查：这种电子产品销售单价定为 $200$ 元时，每天可售出 $300$ 个；若销售单价每降低 $1$ 元，每天可多售出 $5$ 个．已知每个电子产品的固定成本为 $100$ 元，问这种电子产品降价后的销售单价为多少元时，公司每天可获利 $32000$ 元？

查看试题解析
21. 为了激发同学们对理化的科学研究兴趣，并在实践中更好地理解和消化理论知识，提高动手能力，某校在初三年级开展了理化试验操作竞赛，物理、化学图有3个不同的操作实验题目，物理题目用序号①、②、③表示，化学题目用字母a、b、c表示，测试时每名学生每科只操作一个实验，实验的题目由学生随机抽签确定，第一次抽签确定物理实验题目，第二次抽签确定化学实验题目．

(1)、小李同学抽到物理实验题目①这是一个事件（填“必然”、“不可能”或“随机”）．

(2)、小张同学对物理的①、②和化学的c号实验准备得较好，请用画树状图（或列表）的方法，求他同时抽到两科都准备得较好的实验题目的概率．

查看试题解析
22. 如图，四边形ABCD是矩形，AB＝6，BC＝4，点E在边AB上（不与点A、B重合），过点D作DF⊥DE ，交边BC的延长线于点F ．

(1)、求证：△DAE∽△DCF ．

(2)、设线段AE的长为x ，线段BF的长为y ，求y与x之间的函数关系式．

(3)、当四边形EBFD为轴对称图形时，则cos∠AED的值为．

查看试题解析
23.

(1)、【教材呈现】下图是华师版九年级上册数学教材第77页的部分内容．请根据教材提示，结合图1，写出完整的证明过程．
猜想：
如图1．在 $△ A B C$ 中，点 $D$ 、 $E$ 分别是 $A B$ 与 $A C$ 的中点，根据画出的图形，可以猜想：
$D E ∥ B C$ ，且 $D E = \frac{1}{2} B C$ ．
对此，我们可以用演绎推理给证明．

(2)、【结论应用】如图2， $△ A B C$ 是等边三角形，点 $D$ 在边 $A B$ 上（点 $D$ 与点 $A$ 、 $B$ 不重合），过点 $D$ 作 $D E ∥ B C$ 交 $A C$ 于点 $E$ ，连结 $B E$ ， $M$ 、 $N$ 、 $P$ 分别为 $D E$ 、 $B E$ 、 $B C$ 的中点，顺次连结 $M$ 、 $N$ 、 $P$ ．
①求证： $M N = P N$ ；
② $∠ M N P$ 的大小是．

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4$ ， $B C = 3$ ，动点 $P$ 从点 $A$ 出发，沿 $A C$ 以每秒5个单位长度的速度向终点 $C$ 运动，过点 $P$ 作 $P Q ⊥ A B$ 于点 $Q$ ，将线段 $P Q$ 绕点 $P$ 逆时针旋转 $90 °$ 得到线段 $P R$ ，连结 $Q R$ ．设点 $P$ 的运动时间为 $t$ 秒（ $t > 0$ ）．

(1)、线段 $A P$ 的长为（用含 $t$ 的代数式表示）．

(2)、当点 $P$ 与点 $C$ 重合时，求 $t$ 的值．

(3)、当 $C$ 、 $R$ 、 $Q$ 三点共线时，求 $t$ 的值．

(4)、当 $△ C P R$ 为钝角三角形时，直接写出 $t$ 的取值范围．

查看试题解析