吉林省吉林市蛟河市三校联考2023-2024学年九年级上学期数学期末考试试卷

试卷更新日期：2024-02-06 类型：期末考试

进入出卷网下载

一、选择题：本题共6小题，每小题2分，共12分．在每小题给出的选项中，只有一项是符合题目要求的．

1. 如图图形中是中心对称图形的为（　　）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程 $x^{2} - 3 x = 0$ 的解是（　　）

A、 $x = 3$ B、 $x_{1} = 0 ， x_{2} = - 3$ C、 $x_{1} = 0 ， x_{2} = \sqrt{3}$ D、 $x_{1} = 0 ， x_{2} = 3$

查看试题解析
3.
如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m ，CA=0.8m，则树的高度为（）

A、4.8m B、6.4m C、8m D、10m

查看试题解析
4. 在同一平面直角坐标系中，函数y=x﹣1与函数y= $\frac{1}{x}$ 的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
5. 晚上小亮在路灯下散步，在小亮从远处走到灯下，再远离路灯这一过程中，他在地上的影子（　　）

A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长

查看试题解析
6. 如图，一个等边三角形的边长与它的一边相外切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，则这个圆共转了（）

A、4圈 B、3圈 C、5圈 D、3.5圈

查看试题解析

二、填空题：本题共8小题，每小题3分，共24分．

7. 已知关于 $x$ 的方程 $x^{2} + m x - 6 = 0$ 的一个根是 $- 2$ ，则另一个根是.

查看试题解析
8. 小刚的爸爸是养鱼专业户，他想对自己鱼池中的鱼的总数进行评估，第一次捞出 $100$ 条，将每条鱼做出记号放入水中，待它们充分混入鱼群后，又捞出 $200$ 条，且带有记号的鱼有 $5$ 条，其鱼池中估计有鱼条．

查看试题解析
9. 已知 $\frac{a}{b} = \frac{5}{2}$ ，则 $\frac{a - b}{b} =$ .

查看试题解析
10. 两圆的半径分别为 $3$ 和 $5$ ，当这两圆相交时，圆心距 $d$ 的取值范围是．

查看试题解析
11. 已知△ABC，若有|sinA－ $\frac{1}{2}$ |与(tanB $- \sqrt{3}$ )²互为相反数，则∠C的度数是．

查看试题解析
12. 把一张半径为 $2 c m$ ，圆心角为 $120 °$ 的扇形纸片卷成一个圆锥的侧面，那么这个圆锥的底面积是．

查看试题解析
13. 将抛物线 $y = - x^{2}$ 向右平移一个单位，所得函数解析式为

查看试题解析
14. 一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是．

查看试题解析

三、计算题：本大题共1小题，共8分．

15. 某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶.已知看台高为1.6米，现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC（杆子的底端分别为D，C），且∠DAB＝66.5°.

(1)、求点D与点C的高度差DH；

(2)、求所用不锈钢材料的总长度l.（即AD+AB+BC，结果精确到0.1米）
（参考数据：sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30）

查看试题解析

四、解答题：本题共11小题，共76分．解答应写出文字说明，证明过程或演算步骤．

16. 吉万家超市今年的营业额为 $280$ 万元，计划两年后的营业额为 $403.2$ 万元，求平均每年增长的百分率？

查看试题解析
17. 某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．

(1)、当每件的销售价为52元时，该纪念品每天的销售数量为件；

(2)、当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润．

查看试题解析
18. 如图，D、E分别是△ABC的边AB、AC上的点，DE∥BC ， AB＝7，AD＝5，DE＝10，求BC的长．

查看试题解析
19. 如图，把正方形 $A B C D$ 绕点A ，按顺时针方向旋转得到正方形 $A E F G$ ，边 $F G$ 与 $B C$ 交于点H ．求证： $H G = H B$ ．

查看试题解析
20. 已知关于x的方程 $x^{2} + k x - 2 = 0$ 的一个解与方程 $\frac{x + 1}{x - 1} = 3$ 解相同．

(1)、求k的值；

(2)、求方程 $x^{2} + k x - 2 = 0$ 的另一个根．

查看试题解析
21. 甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示．游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．

(1)、用列表法（或画树状图）求甲获胜的概率；

(2)、你认为这个游戏规则对双方公平吗？请简要说明理由．

查看试题解析
22. 如图，同心圆 $O$ ，大圆的面积被小圆所平分，若大圆的弦 $A B$ ， $C D$ 分别切小圆于 $E$ 、 $F$ 点，当大圆半径为 $R$ 时，且 $A B ∥ C D$ ，求阴影部分面积．

查看试题解析
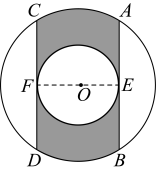23. 如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为格点三角形，图中的△ABC就是格点三角形．在建立平面直角坐标系后，点B的坐标为（-1，-1）．

(1)、把△ABC向左平移8格后得到△A₁B₁C₁ ，画出△A₁B₁C₁的图形，并直接写出点B₁的坐标为；

(2)、把△ABC绕点C按顺时针方向旋转90°后得到△A₂B₂C ，画出△A₂B₂C的图形，并直接写出点B₂的坐标为；

(3)、把△ABC以点A为位似中心，在x轴下方放大，使放大前后对应边长的比为1：2，在方格纸中画出△AB₃C₃的图形．

查看试题解析
24. 已知直线 $y = \frac{1}{2} x + 2$ 与 $x$ 轴、 $y$ 轴交于 $A$ 、 $C$ 两点， $P$ 是该直线上在第一象限内的一点， $P B ⊥ x$ 轴， $B$ 为垂足， $S_{△ A B P} = 9$ ．

(1)、求 $P$ 点的坐标；

(2)、求过 $P$ 点的反比例函数解析式．

查看试题解析
25. 如图，在直角梯形 $A B C D$ 中， $A D ∥ C B$ ， $∠ C = 90 ° ， B C = 16 ， D C = 12 ， A D = 21$ ，动点P从点D出发，沿射线 $D A$ 的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段 $C B$ 上以每秒1个单位长的速度向点B运动，点P ， Q分别从点D ， C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．

(1)、设 $△ B P Q$ 的面积为S ，求S与t之间的函数关系式；

(2)、当t为何值时，四边形 $A B Q P$ 是平行四边形；

(3)、当t为何值时，以B ， P ， Q三点为顶点的三角形是等腰三角形?

查看试题解析
26. 如图，已知抛物线 $y = a x^{2} + \frac{3}{2} x + 4$ 的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．

(1)、求抛物线的解析式和A、B两点的坐标；

(2)、若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；

(3)、若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．

查看试题解析