吉林省白城市大安重点中学2023-2024学年七年级上学期数学期末考试试卷

试卷更新日期：2024-02-06 类型：期末考试

进入出卷网下载

一、选择题：本题共6小题，每小题2分，共12分。在每小题给出的选项中，只有一项是符合题目要求的。

1. $6$ 的倒数是（）

A、 $6$ B、 $- 6$ C、 $\frac{1}{6}$ D、 $- \frac{1}{6}$

查看试题解析
2. 五个大小相同的正方体搭成的几何体如图所示，其从左面看得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $∠ α = 35 °$ ，则 $∠ α$ 的补角的度数为（）

A、 $54 °$ B、 $55 °$ C、 $144 °$ D、 $145 °$

查看试题解析
4. 下列计算正确的是（）

A、 $2 n - 4 n = - 2 n$ B、 $3 a + 2 a = 5 a^{2}$ C、 $3 m + 3 = 6 m$ D、 $7 x^{2} - 6 x^{2} = 1$

查看试题解析
5. 一艘轮船从甲码头到乙码头顺流行驶用 $3$ 小时，从乙码头到甲码头逆流行驶用 $4$ 小时，已知轮船在静水中的速度为 $30$ 千米 $/$ 时，求水流的速度，若设水流的速度为 $x$ 千米 $/$ 时，则列方程正确的是（）

A、 $3 (x + 30) = 4 (x - 30)$ B、 $3 (x + 30) = 4 (30 - x)$ C、 $3 (30 - x) = 4 (x + 30)$ D、 $3 (30 - x) = 4 (30 + x)$

查看试题解析
6. 如图，已知点C是线段 $O A$ 的中点，点B在线段 $A C$ 上，点D是线段 $O B$ 的中点，若线段 $O A = 20 c m$ ，线段 $O B = 12 c m$ ，则线段 $C D$ 的长度为（）

A、 $3 c m$ B、 $4 c m$ C、 $4.5 c m$ D、 $5 c m$

查看试题解析

二、填空题：本题共8小题，每小题3分，共24分。

7. 节约是一种传统美德，节约也是一种智慧，据不完全统计，全国每年浪费粮食总量折合粮食可养活约 $350000000$ 人，用科学记数法表示为．

查看试题解析
8. 用代数式表示：今年小丽 $a$ 岁，她的数学老师的年龄比小丽年龄的 $3$ 倍小 $2$ 岁，小丽数学老师今年岁．

查看试题解析
9. 在多媒体教室的墙上装一幅投影幕布，至少需个钉子，理由是．

查看试题解析
10. 若 $- x^{6} y^{2 m}$ 与 $x^{n + 2} y^{4}$ 的和为 $0$ ，那么 $n + m$ 的值为．

查看试题解析
11. 将 $28 ° 36'$ 用度表示为 $° .$

查看试题解析
12. 下午 $2$ 点整时，时针与分针所组成的角为度 $.$

查看试题解析
13. 当 $x =$ 时，式子 $1 - x$ 与 $\frac{x - 4}{2}$ 的值相等．

查看试题解析
14. 对于两个不相等的有理数 $a$ ， $b$ ，我们规定符号 $m a x {a ， b}$ 表示 $a$ ， $b$ 两数中较大的数，例如 $m a x {2 ， - 4} = 2 .$ 按照这个规定，方程 $m a x {x ， - x} = 2 x + 1$ 的解为．

查看试题解析

三、解答题：本题共12小题，共84分。解答应写出文字说明，证明过程或演算步骤。

15. 计算： $- 4^{2} \times (- 2) + [(- 2)^{3} - (- 4)]$

查看试题解析
16. 先化简，再求值， $5 x^{2} - 7 x - [3 x^{2} - 2 (- x^{2} + 4 x - 1)]$ ，其中 $x = 2$ ．

查看试题解析
17. 解方程： $\frac{x + 3}{2} - 1 = 2 x - \frac{5 - x}{4}$ ．

查看试题解析
18. 已知 $A$ ， $B$ ， $C$ ， $D$ 四点 $($ 如图 $)$ ．

(1)、画线段 $A B$ ，射线 $A D$ ，直线 $A C$ ；

(2)、连接 $B D$ ， $B D$ 与直线 $A C$ 交于点 $E$ ．

查看试题解析
19. 冉冉解方程 $- 3 (★ - 9) = 5 x - 1$ 时，发现 $★$ 处一个常数被涂抹了，已知方程的解是 $x = 5$ ，求 $★$ 处的数字．

查看试题解析
20. 在 $- 2.5$ ， $(- 1)^{2}$ ， $2$ ， $- | - 0.5 |$ ， $- (- 3)$ 中，最小的数是 $a$ ，绝对值最小的数是 $b .$ 求 $- b x + a = 0$ 中 $x$ 的值．

查看试题解析
21. 如图，射线 $O A$ 的方向是北偏东 $15 °$ ，射线 $O B$ 的方向是北偏西 $40 °$ ， $O A$ 是 $∠ B O C$ 的平分线，射线 $O D$ 是 $O B$ 的反向延长线．

(1)、射线 $O D$ 的方向是；

(2)、在图中画出表示南偏东 $75 °$ 的射线 $O E$ ；

(3)、在 $(2)$ 的条件下，求 $∠ C O E$ 的度数．

查看试题解析
22. 如图是一个长方体纸盒的平面展开图，纸盒中相对两个面上的数互为相反数．

(1)、填空： $a =$ ， $b =$ ， $c =$ ；

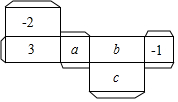(2)、先化简，再求值： $5 a^{2} b - [3 a^{2} b - 2 (3 a b c^{2} - a^{2} b) + 4 a b c^{2}] .$

查看试题解析
23. 请按要求完成下列问题．
如图： $A$ 、 $B$ 、 $C$ 、 $D$ 四点在同一直线上，若 $A B = C D$ ．

(1)、比较线段的大小： $A C$ $B D ($ 填“ $>$ ”、“=”或“ $<$ ” $)$ ；

(2)、若 $B C = \frac{3}{4} A C$ ，且 $A C = 12 c m$ ，求 $A D$ 的长．

查看试题解析
24. 某车间为提高生产总量，在原有 $16$ 名工人的基础上，新调入若干名工人，使得调整后车间的总人数是调入工人人数的 $3$ 倍多 $4$ 人．

(1)、求调入多少名工人；

(2)、在 $(1)$ 的条件下，每名工人每天可以生产 $240$ 个螺栓或 $400$ 个螺母， $1$ 个螺栓需要 $2$ 个螺母，为使每天生产的螺栓和螺母刚好配套，应该安排生产螺栓和螺母的工人各多少名？

查看试题解析
25. 如图，把直角三角形 $M O N$ 的直角顶点 $O$ 放在直线 $A B$ 上 $.$ 射线 $O C$ 平分 $∠ A O N$ ．

(1)、若 $△ M O N$ 的位置如图 $1$ 所示．
$① ∠ M O C = 28 ° .$ 求 $∠ B O N$ 的度数；
$②$ 若 $∠ M O C = m °$ ，则 $∠ B O N$ 的度数为 $($ 用含 $m$ 的式子表示 $)$ ；

(2)、若将图 $1$ 中三角形 $M O N$ 绕点 $O$ 旋转到如图 $2$ 所示的位置，试问 $∠ M O C$ 和 $∠ B O N$ 之间的数量关系是否发生变化？请说明理由．

查看试题解析
26. 如图所示，数轴上点 $A$ ， $B$ 表示的数分别为 $2$ ， $- 8$ ．

(1)、 $A$ ， $B$ 两点之间的距离是； $A$ ， $B$ 两点的中点所表示的数是；

(2)、有一动点 $P$ 从点 $B$ 出发，以每秒 $2$ 个单位长度的速度沿射线 $B A$ 运动，点 $M$ 为 $B P$ 中点，设点 $P$ 运动的时间为 $t$ ，则点 $P$ 表示的数为；点 $M$ 表示的数为．

(3)、 $①$ 当 $t$ 为何值的时候，满足 $A P = B M$ ？
$②$ 若点 $N$ 是 $A P$ 的中点，在 $P$ 点运动的过程中，线段 $M N$ 的长度是否发生变化？若不变，请求出具体的数值；若变化，请说明理由．

查看试题解析