高中数学三轮复习(直击痛点):专题11向量极化恒等式
试卷更新日期:2024-02-05 类型:三轮冲刺
一、选择题
-
1. 中, , 则的取值范围是( )A、 B、 C、 D、2. 已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则 •( + )的最小值是( )A、﹣2 B、﹣ C、﹣ D、﹣13. 在边长为1的正三角形ABC中, =x , =y ,x>0,y>0,且x+y=1,则 • 的最大值为( )A、 B、 C、 D、4. 已知 是边长为4的等边三角形, 为平面 内一点,则 的最小值是( )A、 B、 C、 D、5. 已知向量 ,在 轴上有一点 ,使 有最小值,则 点坐标为( )A、 B、 C、 D、
二、多项选择题
-
6. 已知三个内角A,B,C的对应边分别为a,b,c,且 , . ( )A、面积的最大值为 B、的最大值为 C、的取值范围为 D、7. 如图,底面为边长是2的正方形,半圆面底面.点P为半圆弧上(不含A,D点)的一动点.下列说法正确的是( )
 A、的数量积恒为0 B、三棱锥体积的最大值为 C、不存在点P,使得 D、点A到平面的距离取值范围为
A、的数量积恒为0 B、三棱锥体积的最大值为 C、不存在点P,使得 D、点A到平面的距离取值范围为三、填空题
-
8. 如图,在四边形中, , , , , , 则;设 , 则 .
 9. 窗花是贴在窗子或窗户上的剪纸,是中国古老的传统民间艺术之一,图1是一个正八边形窗花隔断,图2是从窗花图中抽象出的几何图形的示意图.如图2,若正八边形边长为2,是正八边形八条边上的动点,则的取值范围是.
9. 窗花是贴在窗子或窗户上的剪纸,是中国古老的传统民间艺术之一,图1是一个正八边形窗花隔断,图2是从窗花图中抽象出的几何图形的示意图.如图2,若正八边形边长为2,是正八边形八条边上的动点,则的取值范围是.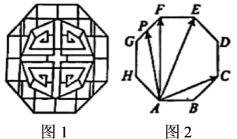 10. 在边长为2的等边中,为的中点,为边上一动点,则的最小值为.11. 向量在向量上的投影向量为 , 则的最大值为 .12. 已知、是平面内两个互相垂直的单位向量,若满足 , 则的最大值为.13. 在中, , , , 为所在平面内的动点,且 , 则的取值范围是 .14. 如图,在矩形ABCD中,AB=2BC=2,AC与BD的交点为M,N为边AB上任意一点(包含端点),则的最大值为 .
10. 在边长为2的等边中,为的中点,为边上一动点,则的最小值为.11. 向量在向量上的投影向量为 , 则的最大值为 .12. 已知、是平面内两个互相垂直的单位向量,若满足 , 则的最大值为.13. 在中, , , , 为所在平面内的动点,且 , 则的取值范围是 .14. 如图,在矩形ABCD中,AB=2BC=2,AC与BD的交点为M,N为边AB上任意一点(包含端点),则的最大值为 . 15. 已知平面向量 , , 且 , , 向量满足 , 则的最小值为.16. 四边形中,点分别是的中点, , 点满足 , 则的最大值为 .17. 若向量 , 满足: , , , 则.18. 已知外接圆的圆心为是边上一动点,若 , 则的最大值为.19. 已知单位向量 , 的夹角为120°,则 = , | ﹣ |(λ∈R)的最小值为 .20. 已知 , 为单位向量,且 • =0,若向量 满足| ﹣( )|=| |,则| |的最大值是 .
15. 已知平面向量 , , 且 , , 向量满足 , 则的最小值为.16. 四边形中,点分别是的中点, , 点满足 , 则的最大值为 .17. 若向量 , 满足: , , , 则.18. 已知外接圆的圆心为是边上一动点,若 , 则的最大值为.19. 已知单位向量 , 的夹角为120°,则 = , | ﹣ |(λ∈R)的最小值为 .20. 已知 , 为单位向量,且 • =0,若向量 满足| ﹣( )|=| |,则| |的最大值是 .四、解答题
-
21. 已知椭圆的左焦点为 , 左、右顶点及上顶点分别记为 , 且 .(1)、求椭圆的方程;(2)、若直线与椭圆交于两点,求面积的最大值,以及取得最大值时直线的方程.