四川省达州市渠县2023-2024学年七年级上学期期末数学测试题

试卷更新日期：2024-02-05 类型：期末考试

进入出卷网下载

一、单项选择题（每小题4分，共40分）

1. $- 2024$ 的绝对值是（）

A、2024 B、 $- 2024$ C、 $\frac{1}{2024}$ D、 $- \frac{1}{2024}$

查看试题解析
2. 下列调查中，宜采用抽样调查的是（）

A、了解全班学生的期末考试数学成绩情况 B、调查“福建号”航母的机器零件情况 C、了解一沓钞票中假钞情况 D、调查长江流域水质情况

查看试题解析
3. 据国家统计局预测，截止2024年底，我国GDP将突破23万亿美元，23万亿用科学记数法表示为（）

A、 $2.3 \times 1 0^{13}$ B、 $2.3 \times 1 0^{14}$ C、 $0.23 \times 1 0^{14}$ D、 $23 \times 1 0^{12}$

查看试题解析
4. 如图是一个正方体的平面展开图，在该正方体中，与“爱”所在面相对面上的字是（）

A、国 B、诚 C、友 D、信

查看试题解析
5. 下列各式中，运算正确的是（）

A、 $3 a - 2 a = 1$ B、 $- 5 b^{2} - 3 b^{2} = - 2 b^{2}$ C、 $x y + 4 y x = 5 x y$ D、 $- 4 (m - 1) = - 4 m - 4$

查看试题解析
6. 下列语句中，正确的个数是（）
①两点确定一条直线；②画射线 $A B = 4 c m$ ；③两点之间，直线最短；④用一个平面截正方体，截面可能是梯形．

A、0 B、1 C、2 D、3

查看试题解析
7. 钟面上显示为3点30分时，时针与分针的夹角是（）

A、 $60 °$ B、 $90 °$ C、 $85 °$ D、 $75 °$

查看试题解析
8. 若 $m - 2 n = 5$ ，则代数式 $1 - 6 n + 3 m$ 的值是（）

A、 $- 14$ B、16 C、6 D、 $- 4$

查看试题解析
9. 若 $| a - 3 | = 2$ ，则 $a =$ （）

A、 $1$ 或 $5$ B、 $- 1$ 或 $- 5$ C、 $- 1$ 或 $5$ D、 $2$ 或 $4$

查看试题解析
10. 某服装店售出两件衣服，每件售价为60元．其中一件赚了20%，另一件亏了20%，那么这家服装店（）

A、赚了10元 B、亏了5元 C、赚了5元 D、不亏不赚

查看试题解析

二、填空题（每小题4分，共20分）

11. 多项式 $- x^{2} y^{4} + 2 x^{2} y^{2} + 2$ 的最高次项的系数是．

查看试题解析
12. 若 $x = - 3$ 是方程 $2 m = 3 + 5 x$ 的解，则 $m$ 的值为．

查看试题解析
13. 如图，在数轴上点 $A$ ，点 $B$ 表示的数分别是 $- 5$ ， $3$ ，点 $P$ 在数轴上，若 $P A = 3 P B$ ，则点 $P$ 表示的数是．

查看试题解析
14. “九宫格”源于我国古代的“洛書”，是世界上最早的“幻方”．在如图的“九宫格”中，把 $1 ~ 9$ 这 $9$ 个整数填入 $3 \times 3$ 方格里，使其任意一行，任意一列及两条对角线上的三个数之和都相等，则 $x$ 的值为．

$4$

$5$
$3$
$6$
$x$

查看试题解析
15. 如图，在长方形ABCD的边上有P ， Q两个动点，速度分别为 $3 c m / s$ ， $1 c m / s$ ，两个点同时出发，运动过程中，一个点到达终点停止运D动时，另一个点也停止运动，动点P从C点出发，沿折线 $C \to B \to A$ 向终点A运动，动点Q从A点出发，沿射线 $A B$ 向终点B运动，运动时间为t秒．若AB=8m， $B C = 4 m$ ，当 $△ B P D$ 和 $△ A Q C$ 的面积之和为12平方米时，t的值为．

查看试题解析

三、解答题：解答时应写出必要的文字说明、证明过程或演算步骤（共90分）

16. 计算题：

(1)、 $3 - 5 - | 4 - 6 | + 2$ ；

(2)、 $- 1^{2024} + 8 \div {(- \frac{2}{3})}^{3} \times | 2023 - 2024 |$ ．

查看试题解析
17. 解方程：

(1)、 $5 x - 14 = 7 - 2 x$ ；

(2)、 $\frac{x - 2}{2} - \frac{3 - x}{5} = 4$

查看试题解析
18. 如图，下面的几何体是由若干棱长为1cm的小立方块搭成．

(1)、从正面、左面、上面观察该几何体，分别画出你所看到的几何体的形状图．

(2)、这个几何体的表面积为cm² ．

查看试题解析
19. 为了庆祝成都大运会胜利闭幕，我市某中学举行了大运会相关知识的竞赛．赛后随机抽查部分参赛同学成绩（满分为100分），并制作成图表如下：
分数段
频数
频率
$60 \leq x < 70$
60
0.15
$70 \leq x < 80$
$m$
0.45
$80 \leq x < 90$
120
$n$
$90 \leq x < 100$
40
0.1
请根据以上图表提供的信息，解答下列问题：

(1)、这次随机抽查了名学生；表中的数 $n =$ ．

(2)、请在图中补全频数分布直方图；

(3)、若绘制扇形统计图，分数段 $60 \leq x < 70$ 所对应扇形的圆心角的度数是．

(4)、全校共有600名学生参加比赛，估计该校成绩不低于80分的学生有多少人？

查看试题解析
20. 如图，数轴上有 $a$ ， $b$ ， $c$ 三点．

(1)、 $c - b$ $0$ ， $c + 1$ $0$ ， $a + c$ $0$ ；(填“ $<$ ”“ $=$ ”，“ $>$ ”)

(2)、化简 $| c - b | + 2 | c + 1 | - | a + c |$ ．

查看试题解析
21. 如图，已知点C在线段 $A B$ 上，点M ， N分别是 $A C$ ， $B C$ 的中点．

(1)、若线段 $A C = 12$ 厘米， $B C = 6$ 厘米，求线段 $M N$ 的长度；

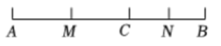(2)、若 $M N = 3 a$ ，其他条件不变，求 $A B$ 的长度（结果用含字母a的代数式表示）．

查看试题解析
22. 已知 $A = m - n$ ， $B = - m + 2 n + 1$ ．

(1)、化简 $2 (A + B) - (A - B)$ （结果用含 $m$ ， $n$ 的代数式表示）；

(2)、已知 $| m + \frac{1}{2} | + {(n - 1)}^{2} = 0$ ，求（ $1$ ）中代数式的值．

查看试题解析
23. 如图，用同样规格的黑白两色的正方形瓷砖铺设长方形地面，请观察下列图形并解答有关问题：

(1)、第 $99$ 个图形中，第一行共有块瓷砖，第一列共有块瓷砖，该图中白色瓷砖共有块．

(2)、第 $n$ 个图形中，铺设地面所用黑色瓷砖的块数为． (用含 $n$ 的代数式表示)

查看试题解析
24. 2023年9月23日，第19届亚洲夏季运动会在杭州举行，象征杭州三大世界文化遗产的吉祥物“宸宸”“琮琮”“莲莲”通过不同颜色、不同纹饰向世界讲述“江南忆”的美丽故事．某网站代售吉祥物和门票，每张门票定价1200元，吉祥物每套定价300元，该网站面向客户提供两种优惠方案．
方案一：买一张门票送一套吉祥物；
方案二：门票和吉祥物都按定价的90%付款．
现某客户要购买门票3张，吉祥物x套( $x > 3$ )．

(1)、若该客户按方案一购买，需付款（）元（用含x的式子表示）；若该客户按方案二购买，需付款（）元（用含x的式子表示）

(2)、若 $x = 5$ ，通过计算说明此时按哪种方案购买较为合算？

(3)、当 $x = 5$ 时，你能给出一种更为省钱的购买方案吗？请直接写出你的购买方案，并算出所需费用．

查看试题解析
25. 如图1，已知 $∠ A O B = 120 °$ ，射线 $O P$ 从 $O A$ 位置出发，以每秒 $2 °$ 的速度按顺时针方向向射线 $O B$ 旋转；与此同时，射线 $O Q$ 从 $O B$ 位置出发以每秒 $4 °$ 的速度绕点O按逆时针方向向射线 $O A$ 旋转，到达射线 $O A$ 后又以同样的速度绕点O按顺时针方向返回，当射线 $O P$ 与射线 $O B$ 重合时，两条射线同时停止运动，设旋转时间为 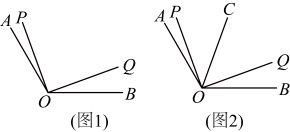$t (s)$ ．

(1)、当 $t = 5$ 时，求 $∠ P O Q$ 的度数；

(2)、当 $∠ P O Q = 60 °$ 时，求t的值；

(3)、如图2，在旋转过程中，若射线 $O C$ 始终平分 $∠ A O Q$ ，问：是否存在t的值，使得 $∠ P O Q = \frac{1}{2} ∠ C O Q$ ？若存在，请直接写出t的值；若不存在，请说明理由．

查看试题解析

分数段	频数	频率
$60 \leq x < 70$	60	0.15
$70 \leq x < 80$	$m$	0.45
$80 \leq x < 90$	120	$n$
$90 \leq x < 100$	40	0.1

		$4$
	$5$	$3$
$6$	$x$