广东省汕尾市陆丰市2023年中考二模数学试卷

试卷更新日期：2024-02-04 类型：中考模拟

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 下列各数中，属于正数的是（）

A、+（﹣2） B、﹣3的相反数 C、﹣（﹣a） D、3﹣a

查看试题解析
2. 下列四句话中的文字有三句具有对称规律，其中没有这种规律的一句是（）

A、上海自来水来自海上 B、有志者事竟成 C、清水池里池水清 D、蜜蜂酿蜂蜜

查看试题解析
3. 《国语》有云：“夫美也者，上下、内外、小大、远近皆无害焉，故曰美．”这是古人对于对称美的一种定义，这种审美法则在生活中体现得淋漓尽致．在下列扬州剪纸图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 中国信息通信研究院测算，2020～2025年，中国5G商用带动的信息消费规模将超过8万亿元，直接带动经济总产出达10.6万亿元．其中数据10.6万亿用科学记数法表示为（）

A、10.6×10⁴ B、1.06×10¹³ C、10.6×10¹³ D、1.06×10⁸

查看试题解析
5. 下列运算正确的是（　　）

A、a+a＝a² B、a²•a³＝a⁵ C、（ab）²＝ab² D、（a²）³＝a⁵

查看试题解析
6. 有一组从小到大排列的数据：1，3，3，x ， 6，下列结论中，正确的是（）

A、这组数据可以求出极差 B、这组数据的中位数不能确定 C、这组数据的众数是3 D、这组数据的平均数可能是3

查看试题解析
7. 关于x的不等式 $\frac{x - 2}{3} > \frac{x}{2}$ ﹣1的解集是（）

A、x＞2 B、x＜2 C、x＜﹣2 D、x＞﹣2

查看试题解析
8. 如图，在扇形AOB中，∠AOB＝130°，OA＝3，若弦BC∥AO ，则 $\hat{A C}$ 的长为（）

A、 $\frac{5 π}{12}$ B、 $\frac{2 π}{3}$ C、 $\frac{5 π}{6}$ D、 $\frac{4 π}{3}$

查看试题解析
9. 如图，BD为 $▱ A B C D$ 的对角线，分别以B，D为圆心，大于 $\frac{1}{2} B D$ 的长为半径作弧，两弧相交于两点，过这两点的直线分别交AD，BC于点E，F，交BD于点O，连接BE，DF．根据以上尺规作图过程，下列结论不一定正确的是（）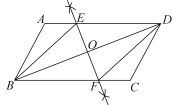

A、点O为 $▱ A B C D$ 的对称中心 B、BE平分 $∠ A B D$ C、 $S_{△ A B E} ： S_{△ B D F} = A E ： E D$ D、四边形BEDF为菱形

查看试题解析
10. 为了锻炼学生身体素质，训练定向越野技能，某校在一公园内举行定向越野挑战赛．路线图如图1所示，点E为矩形ABCD边AD的中点，在矩形ABCD的四个顶点处都有定位仪，可监测运动员的越野进程，其中一位运动员P从点B出发，沿着B﹣E﹣D的路线匀速行进，到达点D．设运动员P的运动时间为t，到监测点的距离为y．现有y与t的函数关系的图象大致如图2所示，则这一信息的来源是（　　）

A、监测点A B、监测点B C、监测点C D、监测点D

查看试题解析

二、填空题（共5小题，满分15分，每小题3分）

11. 在式子 $\sqrt{x - 2}$ 中，x的取值范围是.

查看试题解析
12. 分解因式 $m^{2} + 6 m =$ .

查看试题解析
13. 在Rt△ABC中，∠ACB＝90°，CB＝8，点D是AB边上一点，BD＝5， $s i n ∠ D C B = \frac{3}{5}$ ，则AC＝．

查看试题解析
14. 如图，某同学准备用一根内半径为 $5 c m$ 的塑料管裁一个引水槽，使槽口宽度 $A B$ 为 $8 c m$ ，则槽的深度 $C D$ 为 $c m$ ．

查看试题解析
15. 如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，P是△ABC的高CD上一个动点，以B点为旋转中心把线段BP逆时针旋转45°得到BP^' ，连接DP^' ，则DP^'的最小值是．

查看试题解析

三、解答题（共8小题，满分75分）

16. 解方程组： ${\begin{array}{l} 3 x - 2 y = 7 \\ \frac{x - 2}{3} - \frac{2 y - 1}{2} = 1 \end{array}$

查看试题解析
17. 先化简： $\frac{x^{2}}{x - 1}$ ÷（1+ $\frac{1}{x^{2} - 1}$ ），再从绝对值小于2的数中选择一个合适的x代入求值．

查看试题解析
18. 如图，在△ABC中，∠B＝2∠C ，分别以点A ， C为圆心，大于 $\frac{1}{2} A C$ 的长为半径画弧，两弧在AC两侧分别交于P ， Q两点，作直线PQ交BC边于点D ，交AC于点E ， AB＝5，BC＝13，求BD的长．

查看试题解析
19. “小手拉大手，共创文明城”．某校为了解家长对郑州市创建全国文明城市相关知识的知晓情况，通过发放问卷进行测评，从中随机抽取20份答卷，并统计成绩（成绩得分用x表示．单位：分）：94，83，90，86，94，88，96，100，89，82，94，82，84，89，88，93.98，94，93，92．整理上面的数据，得到频数分布表和扇形统计图．
等级
成绩/分
频数
A
95≤x≤100
a
B
90≤x＜100
8
C
85≤x＜90
5
D
80≤x＜85
4
根据以上信息，解答下列问题：

(1)、填空：a＝， b＝；

(2)、若成绩不低于90分为优秀，请估计该校1600名学生中，达到优秀等级的人数；

(3)、已知A等级中有2名男生，现从A等级中随机抽取2名同学，试用列表或画树状图的方法求出恰好抽到一男一女的概率．

查看试题解析
20. 如图，在平面直角坐标系中，一次函数y＝kx+b与反比例函数y＝﹣ $\frac{6}{x}$ 的图象交于A（﹣1，m），B（n ， ﹣3）两点，一次函数y＝kx+b的图象与y轴交于点C ．

(1)、求一次函数的解析式；

(2)、根据函数的图象，直接写出不等式kx+b≤﹣ $\frac{6}{x}$ 的解集；

(3)、点P是x轴上一点，且△BOP的面积等于△AOB面积的2倍，求点P的坐标．

查看试题解析
21. 某中学开学初在商场购进A、B两种品牌的足球，购买A品牌足球花费了2500元，购买B品牌足球花费了2000元，且购买A品牌足球数量是购买B品牌足球数量的2倍，已知购买一个B品牌足球比购买一个A品牌足球多花30元．

(1)、求购买一个A品牌、一个B品牌的足球各需多少元；

(2)、该中学决定再次购进A、B两种品牌足球共50个，恰逢商场对两种品牌足球的售价进行调整，A品牌足球售价比第一次购买时提高了8%，B品牌足球按第一次购买时售价的9折出售，如果这所中学此次购买A、B两种品牌足球的总费用不超过3060元，那么该中学此次最多可购买多少个B品牌足球？

查看试题解析
22. 如图，AB是⊙O的直径，弦CD⊥AB于E ，与弦AF交于G ，过点F的直线分别与AB ， CD的延长线交于M ， N ， FN＝GN ．

(1)、求证：MN是⊙O的切线；

(2)、若BM＝1， $s i n M = \frac{4}{5}$ ，求AF的长．

查看试题解析
23. 如图，抛物线与x轴交于A、B两点（B在A的左边），与y轴交于点C（0，3），顶点为D（﹣1，4）．

(1)、求该抛物线所对应的函数关系式；

(2)、如图，若点P是第二象限内抛物线上的一动点，过点P作PM⊥x轴于点M ，交BC于点E ，连接PC ，是否存在点P ，使得△PCE与△BME相似？若存在，请求出满足条件的点P的坐标；若不存在，请说明理由．

查看试题解析

等级	成绩/分	频数
A	95≤x≤100	a
B	90≤x＜100	8
C	85≤x＜90	5
D	80≤x＜85	4