江苏省南京市鼓楼区2023-2024学年九年级（上）数学月考试卷

试卷更新日期：2024-02-04 类型：月考试卷

进入出卷网下载

一、选择题（本大题共6小题，每小题2分，共12分，在每小题所给出的四个选项中，恰有

1. 已知ab＝cd ，则下列各式不成立的是（）

A、 $\frac{a}{c}$ ＝ $\frac{d}{b}$ B、 $\frac{a}{d}$ ＝ $\frac{c}{d}$ C、 $\frac{a + c}{c}$ ＝ $\frac{a + b}{b}$ D、 $\frac{a + 1}{c + 1}$ ＝ $\frac{d + 1}{b + 1}$

查看试题解析
2. 小明用地理中所学的等高线的知识在某地进行野外考察，他根据当地地形画出了“等高线示意图”，如图所示（注：若某地在等高线上，则其海拔就是其所在等高线的数值；若不在等高线上，则其海拔在相邻两条等高线的数值范围内），若A ， B ， C三点均在相应的等高线上，且三点在同一直线上，则 $\frac{A B}{A C}$ 的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3}{5}$ D、2

查看试题解析
3. 小明沿着坡度为1：2的山坡向上走了1000m，则他升高了( )

A、200 $\sqrt{5}$ m B、500m C、500 $\sqrt{3}$ m D、1000m

查看试题解析
4. 已知二次函数y＝ax²﹣2x+ $\frac{1}{2}$ （a为常数，且a＞0），下列结论：①函数图象一定经过第一、二、四象限；②函数图象一定不经过第三象限；③当x＜0时，y随x的增大而减小；④当x＞0时，y随x的增大而增大．其中所有正确结论的序号是（）

A、①② B、②③ C、② D、③④

查看试题解析
5. 一枚质地均匀的正方体骰子（六个面分别标有数字1，2，3，4，5，6），投掷5次，分别记录每次骰子向上的一面出现的数字．根据下面的统计结果，能判断记录的这5个数字中一定没有出现数字6的是（）

A、中位数是3，众数是2 B、平均数是3，中位数是2 C、平均数是3，方差是2 D、平均数是3，众数是2

查看试题解析
6. 如图，将矩形ABCD沿着GE、EC、GF翻折，使得点A、B、D恰好都落在点O处，且点G、O、C在同一条直线上，同时点E、O、F在另一条直线上．小炜同学得出以下结论：①GF∥EC；② $A B = \frac{4 \sqrt{3}}{5} A D$ ；③ $C E = \sqrt{6} D F$ ；④ $O C = 2 \sqrt{2} O F$ ．其中正确的是（）

A、①②③ B、①③④ C、①④ D、②③④

查看试题解析

二、填空题（本大题共10小题，每题2分，共20分，不需写出解答过程，请把答案直接填

7. 黄金分割比符合人的视觉习惯，在人体躯干和身高的比例上，肚脐是理想的黄金分割点，即比例越接近0.618越给人以美感．张女士身高165cm ，若她下半身的长度（脚底到肚脐的高度）与身高的比值是0.60，为尽可能达到匀称的效果，她应该选择约厘米的高跟鞋看起来更美．（结果保留整数）

查看试题解析
8. 若一个圆锥的底面圆的半径是2，侧面展开图的圆心角的度数是180°，则该圆锥的母线长为．

查看试题解析
9. 已知△ABC∽△DEF ，若△ABC的三边分别长为6，8，10，△DEF的面积为96，则△DEF的周长为．

查看试题解析
10. 某学校举行学生会成员的竞选活动，对竞选者从平时表现、民主测评、和讲演三个方面分别按百分制打分，然后以3：2：5的比例计算最终成绩，若一名同学的平时表现、民主测评、和讲演成绩分别为90分、80分和94分，则这名同学的最终成绩为分．

查看试题解析
11. 如图，在△ABC中，∠C＝90°，AC＝BC ，如果在AB上任取一点M ，那么AM≤AC的概率是．

查看试题解析
12. 如图，四边形ABCD中，∠A＝∠B＝90°，AB＝5cm ， AD＝3cm ， BC＝2cm ， P是AB上一点，若以P、A、D为顶点的三角形与△PBC相似，则PA＝cm ．

查看试题解析
13. 已知a≠b ，且a²﹣13a+1＝0，b²﹣13b+1＝0，那么 $\frac{b}{1 + b} + \frac{a^{2} + a}{a^{2} + 2 a + 1}$ ＝．

查看试题解析
14. 在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y＝x的图象被⊙P截得的弦AB的长为 $2 \sqrt{3}$ ，则a的值是．

查看试题解析
15. 有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图， $∠ A B C = 90 °$ ，点M，N分别在射线 $B A$ ， $B C$ 上， $M N$ 长度始终保持不变， $M N = 4$ ， $E$ 为 $M N$ 的中点，点D到 $B A$ ， $B C$ 的距离分别为4和2．在此滑动过程中，猫与老鼠的距离 $D E$ 的最小值为．

查看试题解析
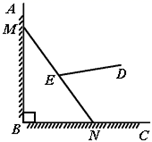16. 如图，Rt△ABC内接于⊙O ， AC＝BC ， ∠BAC的平分线AD与⊙O交于点D ，与BC交于点E ，延长BD ，与AC的延长线交于点F ，连接CD ， G是CD的中点，连接OG ．若OG•DE＝3（2﹣ $\sqrt{2}$ ），则⊙O的面积为．

查看试题解析

三、解答题（本大题共11小题，共88分，请在答题卡指定区域内作答，解答时应写出文字

17. 计算：

(1)、 ${(π - 2)}^{0} - | 1 - t a n 60 ° | - {(\frac{1}{2})}^{- 1} + \frac{6}{\sqrt{3}}$ ；

(2)、sin45°﹣cos30°tan60°．

查看试题解析
18. 解方程：x²﹣4x﹣1=0．

查看试题解析
19. 如图，AD是△ABC的高， $\cos B = \frac{\sqrt{2}}{2} ， \sin C = \frac{3}{5} ， A C = 10$ ，求△ABC的周长.

查看试题解析
20. 张明、李成两位同学初二学年10次数学单元自我检测的成绩（成绩均为整数，且个位数为0）分别如图所示：
利用图中提供的信息，解答下列问题．

(1)、完成下表：
姓名
平均成绩
中位数
众数
方差
张明
80
80
李成
260

(2)、如果将90分以上（含90分）的成绩视为优秀，则优秀率高的同学是；

(3)、根据图表信息，请你对这两位同学各提一条不超过20个字的学习建议．

查看试题解析
21. 二次函数y＝ax²+bx+c的自变量x与函数值y的部分对应值如下表：
x
…
﹣1
0
1
2
3
…
y
…
﹣1
﹣ $\frac{7}{4}$
﹣2
﹣ $\frac{7}{4}$
…
根据表格中的信息，完成下列各题

(1)、当x＝3时，y＝；

(2)、当x＝时，y有最值为；

(3)、若点A（x₁ ， y₁）、B（x₂ ， y₂）是该二次函数图象上的两点，且﹣1＜x₁＜0，1＜x₂＜2，试比较两函数值的大小：y₁y₂

(4)、若自变量x的取值范围是0≤x≤5，则函数值y的取值范围是．

查看试题解析
22. 已知二次函数y＝ax²+bx+2的图象经过点（2，0）和点C ．

(1)、若点C坐标为（1，3），
①求这个二次函数的表达式；
②当﹣1≤x≤2时，直接写出y的取值范围．

(2)、若点C坐标为（1，m）且该函数的图象开口向上，直接写出m的取值范围．

查看试题解析
23. 小明在学完物理“电学”知识后，进行“灯泡亮了”的实验，设计了如图所示的电路图，电路图上有5个开关S₁、S₂、S₃、S₄、S₅和一个小灯泡，当开关S₁闭合时，再同时闭合开关S₂、S₃或S₄、S₅都可以使小灯泡发亮．

(1)、当开关S₁、S₂已经闭合时，再任意闭合开关S₃、S₄、S₅中的一个，小灯泡能亮起来的概率是；

(2)、当开关S₁已经闭合时，再任意闭合开关S₂、S₃、S₄、S₅中的两个，请用列表或画树状图的方法求小灯泡能亮起来的概率．

查看试题解析
24. 如图，已知AB为⊙O的直径，AD ， BD是⊙O的弦，BC是⊙O的切线，切点为B ， OC∥AD ， BA ， CD的延长线相交于点E.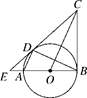

(1)、求证：DC是⊙O的切线；

(2)、若AE＝1，ED＝3，求⊙O的半径．

查看试题解析
25. 如图，在△ABC中，点D、E分别在边AB、AC上，∠AED＝∠B ， AG分别交线段DE、BC于点F、G ，且AD：AC＝DF：CG ．求证：

(1)、AG平分∠BAC；

(2)、EF•CG＝DF•BG ．

查看试题解析
26. 如图1，折叠矩形纸片ABCD，具体操作：①点E为AD边上一点（不与点A，D重合），把△ABE沿BE所在的直线折叠，A点的对称点为F点；②过点E对折∠DEF，折痕EG所在的直线交DC于点G，D点的对称点为H点．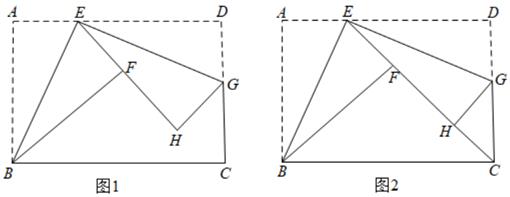

(1)、求证：△ABE∽△DEG．

(2)、若AB=3，BC=5
①点E在移动的过程中，求DG的最大值

②如图2，若点C恰在直线EF上，连接DH，求线段DH的长．

查看试题解析

x	…	﹣1	0	1	2	3	…
y	…	﹣1	﹣ $\frac{7}{4}$	﹣2	﹣ $\frac{7}{4}$		…

姓名	平均成绩	中位数	众数	方差
张明		80	80
李成				260