广西壮族自治区南宁市2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-02-02 类型:期中考试
一、单项选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 的平方根是( )A、±4 B、4 C、±2 D、23. 已知点的坐标为 , 则点关于轴的对称点坐标为( )A、 B、 C、 D、4. 能把一个三角形分成面积相等的两个三角形的是( ).A、高 B、中线和角平分线 C、角平分线 D、中线5. 在中, , 则的度数是( )A、 B、 C、 D、6. 如图,在中, , 是延长线上一点,若 , 则的度数为( )
2. 的平方根是( )A、±4 B、4 C、±2 D、23. 已知点的坐标为 , 则点关于轴的对称点坐标为( )A、 B、 C、 D、4. 能把一个三角形分成面积相等的两个三角形的是( ).A、高 B、中线和角平分线 C、角平分线 D、中线5. 在中, , 则的度数是( )A、 B、 C、 D、6. 如图,在中, , 是延长线上一点,若 , 则的度数为( ) A、40° B、45° C、50° D、55°7. 如图,为线段的垂直平分线上一点,若 , 则的长为( )
A、40° B、45° C、50° D、55°7. 如图,为线段的垂直平分线上一点,若 , 则的长为( )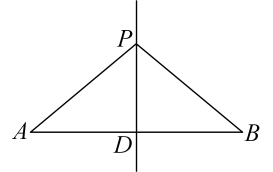 A、 B、 C、 D、8. 如图,在中, , , 点在上, , , 则等于( )
A、 B、 C、 D、8. 如图,在中, , , 点在上, , , 则等于( ) A、1 B、5 C、6 D、89. 如图,为测量池塘两端的距离,学校课外实践小组在池塘旁的开阔地上选了一点C,测得的度数,在的另一侧测得 , , 再测得的长,就是的长.其依据是( )
A、1 B、5 C、6 D、89. 如图,为测量池塘两端的距离,学校课外实践小组在池塘旁的开阔地上选了一点C,测得的度数,在的另一侧测得 , , 再测得的长,就是的长.其依据是( ) A、 B、 C、 D、10. 如图,点、、在同一条直线上, , , , , , , 则的长为( )
A、 B、 C、 D、10. 如图,点、、在同一条直线上, , , , , , , 则的长为( ) A、2 B、3 C、4 D、711. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A、2 B、3 C、4 D、711. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )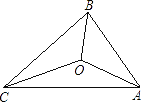 A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:512. 如图,交于点M,交于点D,交于点N, , , , 给出下列结论:①;②;③;④ . 其中正确的结论有( )
A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:512. 如图,交于点M,交于点D,交于点N, , , , 给出下列结论:①;②;③;④ . 其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本大题共6小题,每小题2分,共12分)
-
13. 若n边形的内角和是 , 则n的值为 .14. 如图,在中, , , , 则的长为 .
 15. 如图,一种滑翔伞的形状是左右对称的四边形 , 其中 , 则°.
15. 如图,一种滑翔伞的形状是左右对称的四边形 , 其中 , 则°. 16. 如图,在中, , 于点D,过的中点E作交的延长线于点F,若 , 则的长为 .
16. 如图,在中, , 于点D,过的中点E作交的延长线于点F,若 , 则的长为 .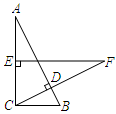 17. 如图,在中, , , 垂直平分 , 点P为直线上的任一点,则周长的最小值是 .
17. 如图,在中, , , 垂直平分 , 点P为直线上的任一点,则周长的最小值是 . 18. 如图,在平面直角坐标系中.对进行循环往复的轴对称变换,若原来点A坐标是 , 则经过第2023次变换后所得的A点坐标是 .
18. 如图,在平面直角坐标系中.对进行循环往复的轴对称变换,若原来点A坐标是 , 则经过第2023次变换后所得的A点坐标是 .
三、解答题(本大题共8小题,共72分,解答应写出文字说明、证明过程或演算步骤)
-
19. 计算: .20. 解不等式组 ,并把它的解集在数轴上表示.
 21. 如图,已知、、是平面直角坐标系中的三点.
21. 如图,已知、、是平面直角坐标系中的三点. (1)、请画出关于x轴对称的;(2)、在x轴上找一点P,并标出点P的位置,使得最小;(3)、若中有一点M坐标为 , 请直接写出经过以上变换后中点M的对应点的坐标为 .22. 如图,点D,E在的边上,连接 , , 若 , , 试证明: .
(1)、请画出关于x轴对称的;(2)、在x轴上找一点P,并标出点P的位置,使得最小;(3)、若中有一点M坐标为 , 请直接写出经过以上变换后中点M的对应点的坐标为 .22. 如图,点D,E在的边上,连接 , , 若 , , 试证明: .圆圆的证明过程如下:
证明:∵ , ∴ ,
在与中,
,
∴ , ∴ .
她的证明过程_▲_(填“正确”“错误”).若不正确,请写出正确的推导过程.
 23. 如图,在等边三角形ABC的三边上,分别取点D,E,F,使得AD=BE=CF求证:△DEF为等边三角形,.
23. 如图,在等边三角形ABC的三边上,分别取点D,E,F,使得AD=BE=CF求证:△DEF为等边三角形,. 24. 萱萱与爸爸妈妈在操场上荡秋千.如图,萱萱坐在秋千上的起始位置A处,起始位置与地面垂直,两脚在地面上用力一蹬,妈妈在B处接住她;妈妈用力一推,爸爸在C处接住她.若妈妈与爸爸到秋千起始位置的水平距离分别为和 , ,
24. 萱萱与爸爸妈妈在操场上荡秋千.如图,萱萱坐在秋千上的起始位置A处,起始位置与地面垂直,两脚在地面上用力一蹬,妈妈在B处接住她;妈妈用力一推,爸爸在C处接住她.若妈妈与爸爸到秋千起始位置的水平距离分别为和 , , (1)、与全等吗?请说明理由;(2)、请求出FG的长.25. 数学课上,老师画出一等腰并标注: , , 然后让同学们提出有效问题并解决.请你结合同学们提出的问题给予解答.
(1)、与全等吗?请说明理由;(2)、请求出FG的长.25. 数学课上,老师画出一等腰并标注: , , 然后让同学们提出有效问题并解决.请你结合同学们提出的问题给予解答. (1)、甲同学提出:如图1,过点C作于点H,可求出;(2)、乙同学提出:的面积为:;(3)、丙同学提出:如图2点D为边的中点, , , 垂足为E、F,请求出的值;(4)、丁同学说受丙同学启发,如图3点D为边上任一点, , , , 垂足为E、F、H,则有 . 请你为丁同学说明理由.26. 如图①,已知点D在线段上,在和中, , , , , 且M为的中点.
(1)、甲同学提出:如图1,过点C作于点H,可求出;(2)、乙同学提出:的面积为:;(3)、丙同学提出:如图2点D为边的中点, , , 垂足为E、F,请求出的值;(4)、丁同学说受丙同学启发,如图3点D为边上任一点, , , , 垂足为E、F、H,则有 . 请你为丁同学说明理由.26. 如图①,已知点D在线段上,在和中, , , , , 且M为的中点. (1)、如图①,连接并延长交于N,与的位置关系为:;线段与的数量关系为:;(2)、在(1)的条件下,判断直线与的位置关系,并说明理由;(3)、将绕点A逆时针旋转,使点E在线段的延长线上(如图②所示位置),(2)中结论是否仍成立?若成立,请证明;若不成立,请说明理由.
(1)、如图①,连接并延长交于N,与的位置关系为:;线段与的数量关系为:;(2)、在(1)的条件下,判断直线与的位置关系,并说明理由;(3)、将绕点A逆时针旋转,使点E在线段的延长线上(如图②所示位置),(2)中结论是否仍成立?若成立,请证明;若不成立,请说明理由.