陕西省西安重点中学2023-2024学年八年级上学期数学第二次月考试卷
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
-
1. 下列方程组中,属于二元一次方程组的是( ).A、 B、 C、 D、2. 用代入法解二元一次方程组时,将方程①代入方程②,得到结果正确的是( )A、 B、 C、 D、3. 若关于、的二元一次方程的一组解为则的值是( )A、 B、2 C、1 D、34. 小明在解关于、的二元一次方程组时,解得则和?代表的数分别是( )A、5和1 B、1和5 C、和3 D、3和5. 如图,函数和的图象交于点 , 点的横坐标为1,则关于 , 的二元一次方程组的解是( )
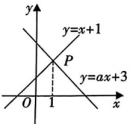 A、 B、 C、 D、6. 小明为了解本班同学一周课外书的阅读量,随机抽取班上20名同学进行调查,调查结果如表,那么这20名同学该周课外书阅读量的平均数是( )
A、 B、 C、 D、6. 小明为了解本班同学一周课外书的阅读量,随机抽取班上20名同学进行调查,调查结果如表,那么这20名同学该周课外书阅读量的平均数是( )阅读量(本/周)
0
1
2
3
4
人数
2
5
4
5
4
A、2本 B、2.2本 C、3本 D、3.2本7. 如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高 , 两块横放的墙砖比两块竖放的墙砖低 , 则每块墙砖的截面面积是( ) A、 B、 C、 D、8. 一次函数的图象过点 , .下列说法不正确的是( )A、图象与轴的交点坐标为 B、图象与轴的交点坐标为 C、随的增大而增大 D、其图象不经过第三象限
A、 B、 C、 D、8. 一次函数的图象过点 , .下列说法不正确的是( )A、图象与轴的交点坐标为 B、图象与轴的交点坐标为 C、随的增大而增大 D、其图象不经过第三象限二、填空题(共5小题,每小题3分,计15分)
-
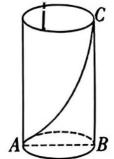
9. 小桐花45元在文具店购买了一些水笔和笔记本,这两种文具的单价分别为7元/支、5元本.设小桐购买了支水笔和本笔记本,根据已知信息,可列出方程为.10. 若某个二元一次方程组的解是 , 则这个方程组可以是.(只要求写出一个)11. 已知一组数据3,7,9,10, , 12的唯一众数是9,则这组数据的中位数是.12. 对于任意实数 , , 定义关于“”的一种运算如下:.例如:.若 , 且 , 则.13. 如图,圆柱的底面周长为10,高 , 是底面直径,动点从点出发,沿着圆柱的侧面移动到点 , 则移动的最短距离为.
三、解答题(共13小题,计81分.解答应写出过程)
-
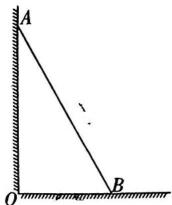
14. 计算:.15. 解二元一次方程组:16. 某校开展主题为“我身边的活雷锋”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得分按的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为90分、80分、90分,则选手甲的最终得分为多少分?17. 若方程是关于的二元一次方程,求的平方根.18. 如图,有一位工人,想测量一面墙上点距离地面的高度 , 他找来一根竹䇯,斜靠在墙上,顶端刚好到达点处,经测量竹䇯的长度为 , 底端远离墙的距离为 , 求点距离地面的高度.
 19. 现有一辆卡车,要运输若干套某种设备,每套设备由部件和部件组成。已知3个部件和2个部件的总质量为7.6吨,5个部件和3个部件的质量相等.求1个部件和1个部件的质量各是多少.20. 已知一组数据:9, , , 8,7,11,7,6的平均数为7,其中 , 求 , 的值21. 如图,在平面直角坐标系中,三个顶点坐标分别为 , , .
19. 现有一辆卡车,要运输若干套某种设备,每套设备由部件和部件组成。已知3个部件和2个部件的总质量为7.6吨,5个部件和3个部件的质量相等.求1个部件和1个部件的质量各是多少.20. 已知一组数据:9, , , 8,7,11,7,6的平均数为7,其中 , 求 , 的值21. 如图,在平面直角坐标系中,三个顶点坐标分别为 , , . (1)、画出关于轴对称的 , 点 , , 的对应点分别是点 , , ;(2)、在(1)的条件下,写出点 , , 的坐标.22. 为弘扬红色文化,传颂红色故事,延安革命老区某学校在八年级开展了红色文化知识竞赛活动,并随机抽取了20名参赛选手的成绩(竞赛成绩均为正数,满分100分)进行统计分析.随机抽取的成绕如下:77,86,80,76,79,100,95,80,75,90,94,86,68,95,88,78,90,82,86,100,整理数据:
(1)、画出关于轴对称的 , 点 , , 的对应点分别是点 , , ;(2)、在(1)的条件下,写出点 , , 的坐标.22. 为弘扬红色文化,传颂红色故事,延安革命老区某学校在八年级开展了红色文化知识竞赛活动,并随机抽取了20名参赛选手的成绩(竞赛成绩均为正数,满分100分)进行统计分析.随机抽取的成绕如下:77,86,80,76,79,100,95,80,75,90,94,86,68,95,88,78,90,82,86,100,整理数据:分数/分
人数/人
2
a
b
5
根据以上信息回答下列问题:
(1)、填空: , .(2)、这20名参赛人员成绩的众数为分,中位数为分;(3)、小李的参赛成绩为88分,你认为他的成绩属于“中上”水平吗?请说明理由.23. 已知关于、的二元一次方程组和关于、的二元一次方程组的解相同,求、的值.24. 甲、乙两家品质相同的红心蜜柚园,销售价格都是每千克12元.两园均推出销售方案,甲收费方案是:游客进园需购买30元的门票,采摘红心蜜柚按原价的七折收费;乙收费方案是:游客进园不需购买门票,采摘超过10千克后,超过部分按六折收费.设某游客的采摘量为千克,甲采摘园所需总费用为元,乙采摘园所需总费用为元.(1)、当采摘量超过10千克时,求 , 与的关系式;(2)、当游客采摘多少千克时,去甲、乙两家采摘园价格相同.(3)、若要采摘30千克,去哪家比较合算?请计算说明.25. 现欲将一批荔枝运往外地销售,若用2辆型车和1辆型车载满荔枝一次可运走10吨;1辆型车和2辆型车载满荔枝一次可运走11吨.现有荔枝31吨,计划同时租用型车辆,型车辆,一次运完,且恰好每辆车都载满荔枝.根据以上信息,解答下列问题:(1)、1辆型车和1辆型车都载满荕枝一次可分别运送多少吨?(2)、请你帮该物流公司设计租车方案.26. 如图,直线的解析式为与轴交于点 , 直线分别与轴,轴交于 , 两点,与直线交于点.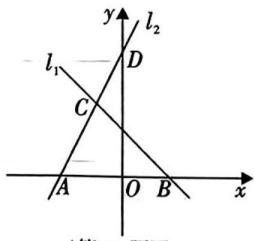 (1)、求点的坐标及直线 , 的解析式;(2)、求的面积;(3)、在上是否存在点 , 使的面积是面积的?若存在,请求出点的坐标;落不存在,请说明理由.
(1)、求点的坐标及直线 , 的解析式;(2)、求的面积;(3)、在上是否存在点 , 使的面积是面积的?若存在,请求出点的坐标;落不存在,请说明理由.