浙江省金华五中2023-2024学年第一学期第三次作业检测七年级数学试卷

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、精心选一选（本题有10个小题，每小题3分，共30分）

1. 在有理数2，-1，0，-5中，最小的数是（）

A、2 B、-1 C、0 D、-5

查看试题解析
2. 整式：0.34x²y，0， $\frac{1}{m n}$ ， x²-y，abc， $\frac{x + 1}{2}$ 中单项式有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 某市2023年的第一季度的财政收入约为84.23亿元，用科学记数法表示为（）

A、84.23×10⁸元 B、8.423×10⁸元 C、8.423×10⁹元 D、0.8423×10¹⁰元

查看试题解析
4. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $\sqrt{36} = \pm 6$ C、 $\sqrt[3]{9} = 3$ D、 $7^{2} \times 7^{3} = 7^{5}$

查看试题解析
5. 下列说法不正确的是（）

A、0既不是正数，也不是负数 B、1是绝对值最小的有理数 C、一个有理数不是整数就是分数 D、0的绝对值是0

查看试题解析
6. 如果 $3 a_{}^{m + 3} b_{}^{4} 与 a_{}^{2} b_{}^{n}$ 同类项，则mn的值为（）

A、4 B、-4 C、8 D、12

查看试题解析
7. 若方程 $(m^{2} - 1) x^{2} + (m - 1) x + 3 = 0$ 是关于x的一元一次方程，则 $m$ 的值是（）

A、 $\pm 1$ B、 $1$ C、 $- 1$ D、 $0$

查看试题解析
8. 下列说法中错误的是（）

A、两点之间线段最短 B、若 $∠ α$ =53°38'，那么 $∠ α$ 余角的度数为36°22' C、一个锐角的余角比这个角的补角小 D、互补的两个角一个是锐角一个是钝角

查看试题解析
9. 小宜跟同学在某餐厅吃饭，如图为此餐厅的菜单．若他们所点的餐点总共为8份意大利面，m杯饮料，n份沙拉，则他们点了几份A餐？（）

A、 $8 - m$ B、 $8 - n$ C、 $8 - m + n$ D、 $8 - m - n$

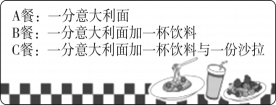查看试题解析
10. 如图，C，D在线段BE上，下列四个说法：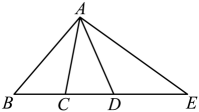
①直线 $C D$ 上以B，C，D，E为端点的线段共有6条；②图中有3对互为补角的角；③若 $∠ B A E = 11 0_{}^{∘} ， ∠ D A C = 4 0_{}^{∘}$ ，则以A为顶点的所有小于平角的角的度数和为370°；④若BC=4，CD=3，DE=5，点F是线段BE上任意一点（包含端点），则点F到点B，C，D，E的距离之和的最小值为15，最大值为23．
其中正确说法的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、耐心填一填（本题有6个小题，每小题4分，共24分）

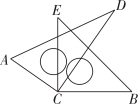
11. $59.12 °$ = ． (结果用度分秒表示）

查看试题解析
12. 若方程 $x + 3 b = 1 与 5 x = 5 + 4 x$ 的解互为相反数，则b的值为．

查看试题解析
13. 12.35精确到0.1：；1249882精确到千位：．

查看试题解析
14. 如图所示，将两块直角三角尺的直角顶点C叠放在一起．若此时量出 $∠ D C E = 3 5_{}^{∘}$ ，则 $∠ A C B$ 的度数为．

查看试题解析
15. 数轴上A ， B两点表示的数分别为-6 ，5，点C是线段AB上的一个动点，以点C为折点，将数轴向左对折，点B的对应点落在数轴上的B'处，若B'A=1，则点C表示的数是．

查看试题解析
16. 有一个长方体水箱，从里面量得它的深度为 $30 c m$ ，底面长为 $25 c m$ ，宽为 $20 c m$ ，水箱里已盛有深度为 $a (c m) (a \leq 30)$ 的水.若往水箱里放入一个棱长为 $10 c m$ 的立方体铁块，则水箱的水深为 $c m$ .

查看试题解析

三、认真答一答（本题有8个小题，共66分）

17. 计算：

(1)、 $- 2^{2} \times \sqrt{{(- 2)}^{2}} - 2$

(2)、 $(\frac{3}{4} - \frac{3}{7} + \frac{3}{14}) \div (\frac{1}{28}) + 3$

查看试题解析
18. 解方程：

(1)、 $10 x + 3 = 12 x - 5$ ；

(2)、 $\frac{3 x - 1}{3} = \frac{4 x + 1}{6} - 1$

查看试题解析
19. 先化简再求值： $- (x^{2} - 6 x y + 9) + 2 (x^{2} + 2 x y)$ ，其中 $x = - 2$ ， $y = \frac{1}{5}$ ．

查看试题解析
20. 如图所示，已知直线l表示一段公路，点A表示学校，点B表示书店，点C表示市图书馆．

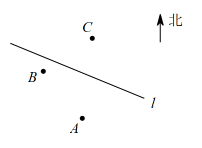(1)、请画出学校A到书店B的最短路线．

(2)、在公路l上找一个路口M ，使得AM+CM的值最小．

(3)、现要从学校A向公路l修一条小路AD ，怎样修路才能使小路AD的长最短？请画出小路AD的路线，并说明作图依据．

查看试题解析
21. 如图，直线AB、CD、MN相交于O ， $F O ⊥ B O$ ， OM平分 $∠ D O F$

(1)、请直接写出图中所有与 $∠ A O N$ 互余的角；

(2)、若 $∠ A O C ： ∠ F O M = 5 ： 2$ ，求 $∠ M O D$ 与 $∠ A O N$ 的度数．

查看试题解析
22. 某市自来水公司为了鼓励居民节约用水，规定按以下标准收取水费：
用水量/月
单价（元/m³）
不超过20 m³
2.05
超过20 m³的部分
3.05
另：每立方米用水加收0.8元的城市污水处理费和0.15元的城市附加费

(1)、根据上表，用水量每月不超过20 m³ ，实际每立方米收水费多少元？如果10月份某用户用水量为18 m³ ，那么该用户10月份应该缴纳水费多少元？

(2)、某用户11月份共缴纳水费80元，那么该用户11月份用水多少立方米？

(3)、若该用户水表12月份出了故障，有25%的水量没有计入水表中，这样该用户在12月份只缴纳了54元水费，问该用户12月份实际应该缴纳水费多少元？

查看试题解析
23. 整体思考是一种重要的解决数学问题的策略．例如：已知当 $x = 1$ 时，代数式 $a x_{}^{3} + b x - 1$ 的值为2024，则当 $x = - 1$ 时，代数式 $a x_{}^{3} + b x + 1$ 的值是多少？
解：∵当 $x = 1$ 时，代数式 $a x_{}^{3} + b x - 1$ 的值为2024，
$∴$ $a + b - 1 = 2024$ $∴$ $a + b = 2025$
当 $x = - 1$ 时， $a x_{}^{3} + b x + 1 = a \times (- 1)_{}^{3} + b \times (- 1) + 1 = - (a + b) + 1 = - 2025 + 1 = - 2024$
请认真阅读上面例题的解答过程，完成下面问题．

(1)、若 $x_{}^{2} + 3 x = 2$ ，则 $2 x_{}^{2} + 6 x - 1 =$ ．

(2)、已知 $m_{}^{2} - n_{}^{2} = 4 ， m n - n_{}^{2} = 1 ，求 m_{}^{2} - 2 m n + n_{}^{2}$ 的值．

(3)、A ， B两地相距60千米，甲、乙两人同时从A ， B两地骑自行车出发，相向而行．甲每小时行a千米，乙每小时行b千米，经过3小时相遇．问甲、乙两人出发多少时间相距10千米．

查看试题解析
24. 已知 $∠ A O B$ ，过顶点O作射线OP ，若 $∠ B O P = \frac{1}{2} ∠ A O P$ ，则称射线OP为 $∠ A O B$ 的“好线”，因此 $∠ A O B$ 的“好线”有两条，如图1，射线OP₁ ， OP₂都是 $∠ A O B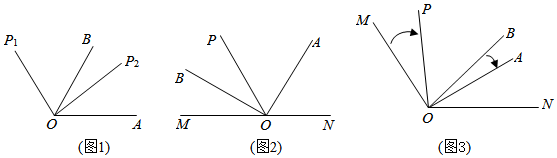$ 的“好线”．

(1)、已知射线OP是 $∠ A O B$ 的“好线”，且 $∠ B O P = 30 °$ ，求 $∠ A O B$ 的度数．

(2)、如图2，O是直线MN上的一点，OB ， OA分别是 $∠ M O P$ 和 $∠ P O N$ 的平分线，已知 $∠ M O B = 30 °$ ，请通过计算说明射线OP是 $∠ A O B$ 的一条“好线”．

(3)、如图3，已知 $∠ M O N = 120 °$ $∠ N O B = 40 °$ ，射线OP和OA分别从OM和OB同时出发，绕点O按顺时针方向旋转，OP的速度为每秒 $20 °$ ， OA的速度为每秒 $4 °$ ，当射线OP旋转到ON ，立即绕点O按逆时针方向旋转，直至射线OA与ON重合时，两条射线同时停止．在旋转过程中，射线OP能否成为 $∠ A O B$ 的“好线”．若不能，请说明理由；若能，请求出符合条件的所有的旋转时间．

查看试题解析

用水量/月	单价（元/m³）
不超过20 m³	2.05
超过20 m³的部分	3.05
另：每立方米用水加收0.8元的城市污水处理费和0.15元的城市附加费