福建省福州市三校2023-2024学年九年级上学期数学月考试卷
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题所给出的四个选项中,只有一个选项是符合题目要求的。
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一元二次方程的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根3. 如图,在中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是( )
2. 一元二次方程的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根3. 如图,在中,P是弦AB的中点,CD是过点P的直径,则下列结论中不正确的是( ) A、 B、 C、 D、4. 下列事件中,属于不可能事件的是( )A、抛掷一枚硬币,落地后正面朝上 B、打开电视机正在播放亚运会比赛 C、在一个只装有白球的袋子里摸出红球 D、正数大于负数5. 反比例函数的图象在每个象限内,y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、6. 已知二次函数的图像上有三点 , , , 则 , , 的大小关系为( )A、 B、 C、 D、7. 函数和在同一平面直角坐标系内的图象大致是( )A、
A、 B、 C、 D、4. 下列事件中,属于不可能事件的是( )A、抛掷一枚硬币,落地后正面朝上 B、打开电视机正在播放亚运会比赛 C、在一个只装有白球的袋子里摸出红球 D、正数大于负数5. 反比例函数的图象在每个象限内,y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、6. 已知二次函数的图像上有三点 , , , 则 , , 的大小关系为( )A、 B、 C、 D、7. 函数和在同一平面直角坐标系内的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 在物理学中,功率表示做功的快慢,功与做功时间的比叫做功率,即所做的功一定时,功率与做功所用的时间成反比例函数关系,图象如图所示,下列说法不正确的是( )
8. 在物理学中,功率表示做功的快慢,功与做功时间的比叫做功率,即所做的功一定时,功率与做功所用的时间成反比例函数关系,图象如图所示,下列说法不正确的是( ) A、P与t的函数关系式为 B、当时, C、当时, D、p随t的增大而减小9. 发动机的曲柄连杆将直线运动转化为圆周运动,图①是发动机的实物剖面图,图②是其示意图.图②中,点A在直线l上往复运动,推动点B做圆周运动形成 , AB与BO表示曲柄连杆的两直杆,点C、D是直线l与的交点;当点A运动到E时,点B到达C;当点A运动到F时,点B到达D.若 , , 则下列结论正确的是( )
A、P与t的函数关系式为 B、当时, C、当时, D、p随t的增大而减小9. 发动机的曲柄连杆将直线运动转化为圆周运动,图①是发动机的实物剖面图,图②是其示意图.图②中,点A在直线l上往复运动,推动点B做圆周运动形成 , AB与BO表示曲柄连杆的两直杆,点C、D是直线l与的交点;当点A运动到E时,点B到达C;当点A运动到F时,点B到达D.若 , , 则下列结论正确的是( ) A、 B、 C、当AB与相切时, D、当时,10. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点 , 点 , 则互异二次函数与正方形OABC有交点时m的最大值和最小值分别是( )
A、 B、 C、当AB与相切时, D、当时,10. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点 , 点 , 则互异二次函数与正方形OABC有交点时m的最大值和最小值分别是( ) A、4, B、 , C、4,0 D、 ,
A、4, B、 , C、4,0 D、 ,二、填空题:本题共6小题,每小题4分,共24分。
-
11. 把二次函数的图象向左平移3个单位长度,再向上平移4个单位长度,平移后二次函数的解析式为.12. 如图是某公园一座抛物线型拱桥,按如图所示建立坐标系,得到函数 , 在正常水位时水面宽米,当水位上升5米时,则水面宽米
 13. 从某小麦新品种的种子中抽取6批,在相同条件下进行发芽实验,数据统计如表:
13. 从某小麦新品种的种子中抽取6批,在相同条件下进行发芽实验,数据统计如表:种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
95
358
744
893
1804
4505
发芽频率
0.950
0.895
0.930
0.893
0.902
0.901
据此可知,该种子发芽的概率为(精确到0.1).
14. 如图,OM为半圆的直径,观察图中的尺规作图痕迹,若 , 则的度数为. 15. 若圆锥的母线长为 , 其侧面积为 , 则圆锥底面半径为 .16. 如图,在平面直角坐标系中,已知点 , 点 , 连接BC , 在第一象限,且与BC和两条坐标轴都相切,反比例函数的图象经过圆心M , 则k的值为.
15. 若圆锥的母线长为 , 其侧面积为 , 则圆锥底面半径为 .16. 如图,在平面直角坐标系中,已知点 , 点 , 连接BC , 在第一象限,且与BC和两条坐标轴都相切,反比例函数的图象经过圆心M , 则k的值为.
三、解答题:本题共9小题,共86分。解答应写出文字说明、证明过程或演算步骤。
-
17. 解方程:18. 已知关于x的一元二次方程x2+(m+2)x+m=0.(1)、求证:无论m取何值,此方程总有两个不相等的实数根;(2)、若方程有两个实数根x1 , x2 , 且x1+x2+2x1x2=1,求m的值.19. 如图,点 , 分别在正方形的边 , 上,且 , 把绕点顺时针旋转得到 .
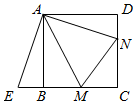 (1)、求证:≌ .(2)、若 , , 求正方形的边长.20. 如图,正方形ABCD内接于⊙O,E是 的中点,连接AE,DE,CE.
(1)、求证:≌ .(2)、若 , , 求正方形的边长.20. 如图,正方形ABCD内接于⊙O,E是 的中点,连接AE,DE,CE. (1)、求证:AE=DE;(2)、若CE=1,求四边形AECD的面积.21. 面向世界的年度文化盛会、四川建设文化强省的闪亮名片——2023天府书展于10月13日至16日在四川成都开幕.本次盛会以“共享书香互鉴文明”为年度主题,定位“书香天府盛典,出版发行盛会”.值得一提的是,成都将为市民举办一场“巴适的购书节”,为庆祝活动的顺利召开,某大型品牌书城购买了A、B两种新出版书籍,商家用1600元购买A书籍,1200元购买B书籍,A、B两种书籍的进价之和为40元,且购买A书籍的数量是B书籍的2倍.(1)、求商家购买A书籍和B书籍的进价.(2)、商家在销售过程中发现,当A书籍的售价为每本25元,B书籍的售价为每本33元时,平均每天可卖出50本A书籍,25本B书籍,据统计,B书籍的售价每降低0.5元平均每天可多卖出5本.商家在保证A书籍的售价和销量不变且不考虑其他因素的情况下,为了促进B的销量,想使A书籍和B书籍平均每天的总获利为775元,则每本B书籍的售价为多少元?22. 如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力×阻力臂=动力×动力臂,如图,即),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆绕支点O在竖直平面内转动,支点O距左端 , 距右端 , 在杠杆左端悬挂重力为80N的物体A.
(1)、求证:AE=DE;(2)、若CE=1,求四边形AECD的面积.21. 面向世界的年度文化盛会、四川建设文化强省的闪亮名片——2023天府书展于10月13日至16日在四川成都开幕.本次盛会以“共享书香互鉴文明”为年度主题,定位“书香天府盛典,出版发行盛会”.值得一提的是,成都将为市民举办一场“巴适的购书节”,为庆祝活动的顺利召开,某大型品牌书城购买了A、B两种新出版书籍,商家用1600元购买A书籍,1200元购买B书籍,A、B两种书籍的进价之和为40元,且购买A书籍的数量是B书籍的2倍.(1)、求商家购买A书籍和B书籍的进价.(2)、商家在销售过程中发现,当A书籍的售价为每本25元,B书籍的售价为每本33元时,平均每天可卖出50本A书籍,25本B书籍,据统计,B书籍的售价每降低0.5元平均每天可多卖出5本.商家在保证A书籍的售价和销量不变且不考虑其他因素的情况下,为了促进B的销量,想使A书籍和B书籍平均每天的总获利为775元,则每本B书籍的售价为多少元?22. 如图所示,是《天工开物》中记载的三千多年前中国古人利用桔槔在井上汲水的情境(杠杆原理:阻力×阻力臂=动力×动力臂,如图,即),受桔槔的启发,小杰组装了如图所示的装置.其中,杠杆绕支点O在竖直平面内转动,支点O距左端 , 距右端 , 在杠杆左端悬挂重力为80N的物体A. (1)、若在杠杆右端挂重物B , 杠杆在水平位置平衡时,重物B所受拉力为N.(2)、为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,的长度随之变化.设重物B的质量为xN,的长度为.则①y关于x的函数解析式是 ▲ .
(1)、若在杠杆右端挂重物B , 杠杆在水平位置平衡时,重物B所受拉力为N.(2)、为了让装置有更多的使用空间,小杰准备调整装置,当重物B的质量变化时,的长度随之变化.设重物B的质量为xN,的长度为.则①y关于x的函数解析式是 ▲ .②完成下表:
…
10
20
30
40
50
…
…
8
a
2
b
…
③在直角坐标系中画出该函数的图象.
 (3)、在(2)的条件下,将函数图象向右平移4个单位长度,与原来的图象组成一个新的函数图象,记为L.若点A的坐标为 , 在L上存在点Q , 使得.请直接写出所有满足条件的点Q的坐标.23. 勾股定理是人类早期发现并证明的重要数学定理之一,至今已有几百种证明方法,在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例;三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释并创制了一幅“勾股圆方图”;后刘徽用“出入相补”原理证明了勾股定理;清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法.(1)、某学校数学活动室进行文化建设,拟从以上4位科学家的画像中随机选用1幅,恰好选中的画像是刘徽的概率;
(3)、在(2)的条件下,将函数图象向右平移4个单位长度,与原来的图象组成一个新的函数图象,记为L.若点A的坐标为 , 在L上存在点Q , 使得.请直接写出所有满足条件的点Q的坐标.23. 勾股定理是人类早期发现并证明的重要数学定理之一,至今已有几百种证明方法,在中国,商朝时期的商高提出了“勾三股四玄五”的勾股定理的特例;三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释并创制了一幅“勾股圆方图”;后刘徽用“出入相补”原理证明了勾股定理;清朝末年,数学家华蘅芳提出了二十多种对于勾股定理证法.(1)、某学校数学活动室进行文化建设,拟从以上4位科学家的画像中随机选用1幅,恰好选中的画像是刘徽的概率;
 (2)、在某次数学活动中,有一个不透明的信封内装有三根长度分别为4cm,6cm和8cm的细木棒,木棒露出纸袋外的部分长度相等,小亮手中有一根长度为cm的细木棒,现从信封内随机取出两根细木棒与小亮手中的细木棒首尾相接放在一起,求抽出的细木棒能与小亮手中的细木棒构成直角三角形的概率(用画树状图或列表的方法求解)24. 已知顶点为A的抛物线过点和.(1)、求点A的坐标;(2)、直线与拋物线相交于不同的两点B , C(B在C的左侧),
(2)、在某次数学活动中,有一个不透明的信封内装有三根长度分别为4cm,6cm和8cm的细木棒,木棒露出纸袋外的部分长度相等,小亮手中有一根长度为cm的细木棒,现从信封内随机取出两根细木棒与小亮手中的细木棒首尾相接放在一起,求抽出的细木棒能与小亮手中的细木棒构成直角三角形的概率(用画树状图或列表的方法求解)24. 已知顶点为A的抛物线过点和.(1)、求点A的坐标;(2)、直线与拋物线相交于不同的两点B , C(B在C的左侧),①若 , 直线AC与x轴相交于D , 连接BD , 求证:轴;
②过点B作不平行y轴的直线 , 且与拋物线有且只有一个公共点.记点P为与x轴的交点;点Q为l与x轴的交点,求线段PQ长度的最小值.(用含a的式子表示)
25. 如图,在等边中,于点 , 为线段上一动点(不与 , 重合),连接 , , 将绕点顺时针旋转得到线段 , 连接 .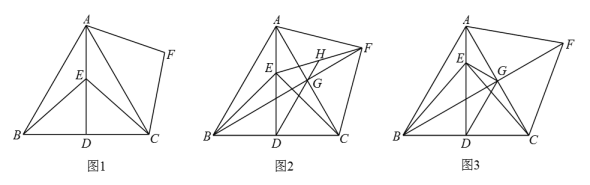 (1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.
(1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.