浙江省宁波市四校联考2023-2024学年九年级上学期12月月考数学试题
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题(每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
-
1. 已知 , 则的值是( )A、 B、 C、 D、2. 已知 , 则的比例中项为( )A、 B、4 C、2 D、3. 在中, , , 那么等于( ).A、 B、 C、 D、4. 两个相似三角形一组对应边上的中线长分别是和 , 且其中较大三角形的周长是 , 则较小三角形的周长为( )A、 B、 C、 D、5. 若为二次函数图象上的三点,则的大小关系为( )A、 B、 C、 D、6. 如图,是的直径,是上的点, , 则的度数是( )
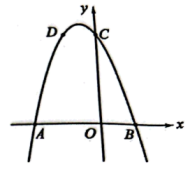
 A、 B、 C、 D、7. 如图,在平面直角坐标系中,与轴相切于原点 , 平行于轴的直线交于两点,若点的坐标是 , 则点的坐标为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,与轴相切于原点 , 平行于轴的直线交于两点,若点的坐标是 , 则点的坐标为( ) A、 B、 C、 D、8. 如图,以为直径的与相切于点B , 连接交于点D , 点E为边中点,连接交于点 . 若的半径为4, . 则的值为( )
A、 B、 C、 D、8. 如图,以为直径的与相切于点B , 连接交于点D , 点E为边中点,连接交于点 . 若的半径为4, . 则的值为( ) A、 B、 C、 D、9. 如图,在锐角中, , , 分别是边上的高线,与交于点F , 则的最大值为( )
A、 B、 C、 D、9. 如图,在锐角中, , , 分别是边上的高线,与交于点F , 则的最大值为( ) A、1 B、 C、 D、10. 规定:若点在某一个函数的图象上,且点的横纵坐标互为相反数,则称点为这个函数的“互反点”.若关于的二次函数对于任意的常数 , 恒有两个“互反点”,则的取值范围为( )A、 B、 C、 D、
A、1 B、 C、 D、10. 规定:若点在某一个函数的图象上,且点的横纵坐标互为相反数,则称点为这个函数的“互反点”.若关于的二次函数对于任意的常数 , 恒有两个“互反点”,则的取值范围为( )A、 B、 C、 D、二、填空题(每小题4分,共24分)
-
11. 抛物线与轴交点坐标是 .12. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点若的顶点均是格点,则的值是 .
 13. 直角三角形的两条直角边长分别为6和8,那么这个三角形的内切圆半径为 .14. 如图,扇形中, , 点分别在上,连接 , 点关于直线对称,的长为 , 则图中阴影部分的面积为 .
13. 直角三角形的两条直角边长分别为6和8,那么这个三角形的内切圆半径为 .14. 如图,扇形中, , 点分别在上,连接 , 点关于直线对称,的长为 , 则图中阴影部分的面积为 . 15. 如图,在正方形中,为上一点,为延长线上一点,且 , 连接交于 , 过作于点 , 连接 . 若 , 则 .
15. 如图,在正方形中,为上一点,为延长线上一点,且 , 连接交于 , 过作于点 , 连接 . 若 , 则 . 16. 如图,在中,是边中点,连接交于点 . 作点关于的对称点 , 若点恰好在射线上, , 则 .
16. 如图,在中,是边中点,连接交于点 . 作点关于的对称点 , 若点恰好在射线上, , 则 .
三、解答题(本大题有6题,共66分)
-
17.(1)、(2)、18. 如图,在平面直角坐标系中,过格点作一圆弧 .
 (1)、所在圆的圆心的坐标为 .(2)、求的长(结果保留)19. 如图是由边长为1的小正六边形构成的网格图,网格上的点称为格点.已知格点线段 , 利用网格图,仅用无刻度的直尺来完成下面几何作图.
(1)、所在圆的圆心的坐标为 .(2)、求的长(结果保留)19. 如图是由边长为1的小正六边形构成的网格图,网格上的点称为格点.已知格点线段 , 利用网格图,仅用无刻度的直尺来完成下面几何作图. (1)、请在图①中作一个格点等腰三角形;(2)、请在图②在线段上求作点 , 使得 . (要求:不写作法但保留作图痕迹)20. 小林在使用笔记本电脑时,为了散热,他将电脑放在散热架CAD上,忽略散热架和电脑的厚度,侧面示意图如图1所示,已知电脑显示屏OB与底板OA的夹角为135°,OB=OA=25cm , OE⊥AD于点E,OE=12.5cm.
(1)、请在图①中作一个格点等腰三角形;(2)、请在图②在线段上求作点 , 使得 . (要求:不写作法但保留作图痕迹)20. 小林在使用笔记本电脑时,为了散热,他将电脑放在散热架CAD上,忽略散热架和电脑的厚度,侧面示意图如图1所示,已知电脑显示屏OB与底板OA的夹角为135°,OB=OA=25cm , OE⊥AD于点E,OE=12.5cm.
 (1)、求∠OAE的度数;(2)、若保持显示屏OB与底板OA的135°夹角不变,将电脑平放在桌面上如图2中的所示,则显示屏顶部比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73, , )21. 如图,是直角三角形, , 点是边上一点,以为直径作交边于点 , 连接 , 且 .
(1)、求∠OAE的度数;(2)、若保持显示屏OB与底板OA的135°夹角不变,将电脑平放在桌面上如图2中的所示,则显示屏顶部比原来顶部B大约下降了多少?(参考数据:结果精确到0.1cm.参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73, , )21. 如图,是直角三角形, , 点是边上一点,以为直径作交边于点 , 连接 , 且 . (1)、求证:直线是的切线;(2)、若 , 求的长.22. 某商店销售进价为40元/件的某种商品,在第天的售价与销量的相关信息如下表:
(1)、求证:直线是的切线;(2)、若 , 求的长.22. 某商店销售进价为40元/件的某种商品,在第天的售价与销量的相关信息如下表:时间(天)
售价(元/件)
80
每天销量(件)
设销售商品的每天利润为元.
(1)、求出与的函数关系式;(2)、问该商品第几天时,当天销售利润最大,最大利润是多少?(3)、现该商店决定每销售1件该商品就捐赠元给贫困地区,在销售的前30天内该商店当日最大利润为2312元,直接写出的值 .