广东省揭阳市揭东区多校联考2023-2024学年七年级上学期数学第二次教学质量监测试题
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题(本大题共10小通,每小题3分,共30分)
-
1. 下列算式计算结果为正数的是( )A、 B、 C、 D、2. 截至2022年5月底,我国手机用户数大约达到6.38亿,将6.38亿用科学记数法可表示为( )A、 B、 C、 D、3. 如图,下列对数轴上A,B两点所表示的两数的关系描述不正确的是( )
 A、两数的绝对值相等 B、两数互为相反数 C、两数的和为0 D、两数的积为14. 图是由几个相同的小立方块搭成的几何体从上面看到的形状图,数字表示该位置上的小立方块的个数,则该几何体从左面看到的形状图是( )
A、两数的绝对值相等 B、两数互为相反数 C、两数的和为0 D、两数的积为14. 图是由几个相同的小立方块搭成的几何体从上面看到的形状图,数字表示该位置上的小立方块的个数,则该几何体从左面看到的形状图是( ) A、
A、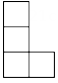 B、
B、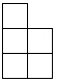 C、
C、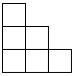 D、
D、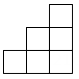 5. 下列变形正确的是( )A、由 , 得 B、由 , 得 C、由, , 得 D、由 , 得6. 有理数在数轴上所对应的点如图所示,则下列结论正确的是( )
5. 下列变形正确的是( )A、由 , 得 B、由 , 得 C、由, , 得 D、由 , 得6. 有理数在数轴上所对应的点如图所示,则下列结论正确的是( )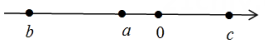 A、 B、 C、 D、7. 对于任意有理数a,b,定义一种新运算“”,规则如下: , 例如: , 则的值为( )A、-11 B、11 C、-29 D、298. 若代数式的值与字母无关,则的值为( )A、2 B、1 C、0 D、-19. 某同学解方程时,把“”处的系数看错了,解得 , 他把“”处的系数看成了( )A、-3 B、3 C、-4 D、410. 已知两个等式 , 则的值为( )A、-3 B、3 C、6 D、-6
A、 B、 C、 D、7. 对于任意有理数a,b,定义一种新运算“”,规则如下: , 例如: , 则的值为( )A、-11 B、11 C、-29 D、298. 若代数式的值与字母无关,则的值为( )A、2 B、1 C、0 D、-19. 某同学解方程时,把“”处的系数看错了,解得 , 他把“”处的系数看成了( )A、-3 B、3 C、-4 D、410. 已知两个等式 , 则的值为( )A、-3 B、3 C、6 D、-6二、填空题(本大题共6小题,每小题3分,共18分)
-
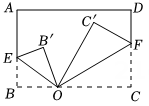
11. 在这四个数中,最小的数是.12. 如果单项式与是同类项,那么(b-a)等于.13. 将一张长方形ABCD纸片按图所示折叠,OE和OF为折痕,点落在点处,点落在点处,若 , 则的度数为.
 14. 已知有理数a,b在数轴上的位置如图,且 , 则关于的方程的解为.
14. 已知有理数a,b在数轴上的位置如图,且 , 则关于的方程的解为.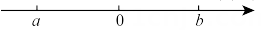 15. 图所示是一个正方体的表面展开图,且相对两个面表示的整式的和都相等.如果 , 那么所代表的整式是.
15. 图所示是一个正方体的表面展开图,且相对两个面表示的整式的和都相等.如果 , 那么所代表的整式是.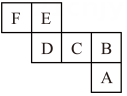 16. 如图是一组有规律的图案,第1个图案中有7个六边形,第2个图案中有13个六边形,第3个图案中有19个六边形……按此规律,第个图案中有个六边形.(用含的代数式表示)
16. 如图是一组有规律的图案,第1个图案中有7个六边形,第2个图案中有13个六边形,第3个图案中有19个六边形……按此规律,第个图案中有个六边形.(用含的代数式表示)
三、解答题(本题共4小题,4分+4分+6分+6分,共20分)
-
17. 计算:;18. 解方程:.19. 先化简,再求值: , 其中.20. 如图,已知线段AB,P是线段AB外一点.
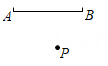 (1)、尺规作图,保留作图痕迹;
(1)、尺规作图,保留作图痕迹;①作射线PA,作直线PB;
②延长线段AB至点 , 使得 , 再反向延长AC至点 , 使得.
(2)、若(1)中的线段 , 求线段BD的长.四、解答题(本题共3小题,8分+10分+10分共28分)
-
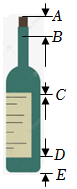
21. 若关于的方程与方程的解互为倒数,求的值.22. 图是一种盛装葡萄酒的瓶子,已量得瓶塞AB与标签CD的高度之比为2:3,且标签底部是BD的中点,又量得 , 求标签CD的高度.
 23. 如图,在同一平面内平分平分.
23. 如图,在同一平面内平分平分.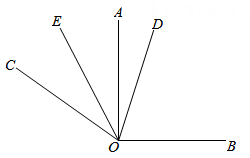 (1)、求的度数;(2)、如果将题日中改成 , 其他条件不变,你能求出的度数鸣?若能,写出求解过程;若不能,请说朋理由.
(1)、求的度数;(2)、如果将题日中改成 , 其他条件不变,你能求出的度数鸣?若能,写出求解过程;若不能,请说朋理由.五、解答题(每小题12分,共24分)
-
24. 甲、乙两家网店分别出售型、型两种取暖器,零售价及运费如下表所示:
零售价
运费
型
型
型
型
甲
100元/台
200元/台
10元/台
10元/台
乙
120元/台
190元/台
免运费
12元/台
某公司计划在网上采购型、型两种取暖器共10台,其中型取暖器购买台.
(1)、若两种取暖器全部在甲店购买,需付总费用为元;若两种取暖器全部在乙店购买,需付总费用为元.(请用含的代数式表示)(2)、当时,请通过计算解决下列问题:①在(1)中的条件下,该公司在哪家网店购买取暖器更划算?
②若两种取暖器可以同时在两家网店自由选择购买,还有比①中更优惠的方案吗?如果有,请写出这个方案,并求出此时购买取暖器的总费用;如果没有,请说明理由.
25. 如图,图一已知数轴上点表示的数为-6,点表示的数为8,动点从出发,以每秒3个单位长度的速度沿射线AB方向向右运动,运动时间为秒.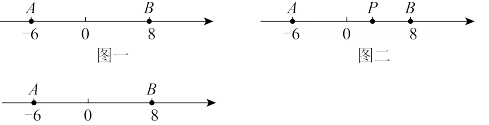 (1)、线段 , 当点运动到线段AB的延长线时.(用含的代数式表示)(2)、如图二,当时,点是AP的中点,点是BP的中点,求此时MN的长.(3)、当点P从出发时,另一个动点同时从点出发,以每秒1个单位长度的速度沿数轴向右运动,存在这样的值,使三点有一点恰好是以另外两点为端点的线段的中点,请求出满足条件的值.
(1)、线段 , 当点运动到线段AB的延长线时.(用含的代数式表示)(2)、如图二,当时,点是AP的中点,点是BP的中点,求此时MN的长.(3)、当点P从出发时,另一个动点同时从点出发,以每秒1个单位长度的速度沿数轴向右运动,存在这样的值,使三点有一点恰好是以另外两点为端点的线段的中点,请求出满足条件的值.