广东省揭阳市2023-2024学年九年级上学期数学期末监测试卷

试卷更新日期：2024-02-02 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题,每小题3分,共30分）

1. 下列关系式中 $y$ 是 $x$ 的反比例函数的是（）

A、 $y = 2 x$ B、 $x y = 1$ C、 $y = \frac{1}{x^{2}}$ D、 $y = \frac{k}{x}$

查看试题解析
2. 如图所示的“中”字，俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 以下列长度（同一单位）为长的四条线段中，成比例的是（）

A、1，2，3，4 B、2，4，8，16 C、2，12，12，4 D、2，10，15，5

查看试题解析
4. 用配方法解一元二次方程 $x^{2} - 8 x - 11 = 0$ 时，下列变形正确的是（）

A、 $(x - 4)^{2} = 5$ B、 $(x + 4)^{2} = 5$ C、 $(x - 4)^{2} = 27$ D、 $(x + 4)^{2} = 27$

查看试题解析
5. 菱形、矩形、正方形都具有的性质是（）

A、两组对边分别平行且相等 B、对角线相等 C、四条边相等，四个角相等 D、对角线互相垂直

查看试题解析
6. 一元二次方程 $2 x^{2} + x - 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
7. 下列关于反比例函数 $y = - \frac{3}{x}$ 的描述中，不正确的是（）

A、图象在第二、四象限 B、 $y$ 随 $x$ 的增大而增大 C、点 $(- 1 ， 3)$ 在反比例函数的图象上 D、当 $x > 1$ 时， $0 > y > - 3$

查看试题解析
8. 在平面直角坐标系中，已知点 $A (- 4 ， 2) ， B (- 6 ， - 4)$ ，以原点 $O$ 为位似中心，相似比为2，把 $△ A B O$ 放大，则点 $B$ 的对应点 $B^{^{'}}$ 的坐标是（）

A、 $(- 3 ， - 2)$ B、 $(- 3 ， - 2)$ 或 $(3 ， 2)$ C、 $(- 12 ， - 8)$ D、 $(- 12 ， - 8)$ 或 $(12 ， 8)$

查看试题解析
9. 如图， $B E$ 是 $△ A B C$ 的中线，点 $D$ 在 $B C$ 上且满足 $C D = 2 B D$ ，连接 $A D$ ，与 $B E$ 交于点 $F$ ，则 $\frac{S_{△ A B C}}{S_{△ A E F}}$ 的值为（）

A、 $\frac{10}{3}$ B、 $\frac{11}{3}$ C、4 D、 $\frac{9}{2}$

查看试题解析
10. 如图，在正方形ABCD外取一点 $E$ ，连接AE、BE、DE.过点 $A$ 作AE的垂线交DE于点 $P$ .若 $A E = A P = 1 ， P B = \sqrt{5}$ .下列结论：① $△ A P D ≅ △ A E B$ ；②点 $B$ 到直线AE的距离是 $\sqrt{2}$ ；③ $E B ⊥ E D$ ；④ $S_{正方形 A B C D} = 4 + \sqrt{6}$ .其中正确的结论是（）

A、①② B、①④ C、①③④ D、①②③

查看试题解析

二、填空题(本大题共5小题,每小题3分,共15分)

11. 太阳光线下形成的投影是投影．（平行或中心）

查看试题解析
12. 若 $5 a = 3 b (a 、 b$ 均不为0)，那么 $b ： a =$ .

查看试题解析
13. 一个盒子中装有20颗蓝色幸运星，若干颗红色幸运星和15颗黄色幸运星，小明通过多次摸取幸运星试验后发现，摸取到红色幸运星的频率稳定在0.5左右，则摸到红色幸运星颗数约为颗.

查看试题解析
14. 如图，点 $P$ 是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上任意一点，过点 $P$ 作 $P M ⊥ x$ 轴，垂足为 $M$ ，若 $△ P O M$ 的面积等于3，则 $k$ 的值为.

查看试题解析
15. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ，过点 $O$ 作 $O E ⊥ B D$ ，交 $B C$ 于点 $E$ ，若 $C O = \sqrt{3}$ ， $C E = 1$ ，则 $B E$ 的长为.

查看试题解析

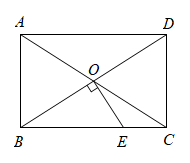
三、解答题(一)(本大题共3小题，每小题8分，共24分)

16. 解方程

(1)、x²-4x+2=0；

(2)、2x²+5=7x

查看试题解析
17. 如图，在 $△ A B C$ 中，点D、E分别在边AC、AB上， $A B =$ $2 A D ， A C = 2 A E$ .
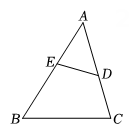
求证： $△ A D E ~ △ A B C$ .

查看试题解析
18. 如图是分别从正面、左面、上面观察一个几何体得到的图形，请解答以下问题：

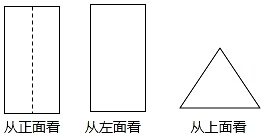(1)、这个几何体的名称为；

(2)、若从正面看到的是长方形，其长为 $10 c m$ ；从上面看到的是等边三角形，其边长为 $4 c m$ ，求这个几何体的侧面积．

查看试题解析

四、解答题(二)(本大题共3小题,每小题9分,共27分)

19. 学习习近平总书记关于生态文明建设重要讲话，牢固树立“绿水青山就是金山银山”的科学观，让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况，对本班全体学生进行了调查，并将调查结果分为三类：A：好，B：中， $C$ ：差.请根据图中信息，解答下列问题：

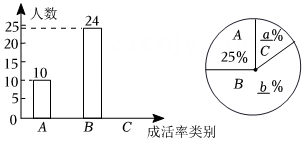(1)、求全班学生总人数；

(2)、在扇形统计图中， $a =$ ， $b =$ ， $C$ 类的圆心角为；

(3)、张老师在班上随机抽取了4名学生，其中 $A$ 类1人， $B$ 类2人， $C$ 类1人，若再从这4人中随机抽取2人，请用列表法或画树状图的方法求出全是 $B$ 类学生的概率.

查看试题解析
20. 某农场要建一个矩形动物场，场地的一边靠墙(墙AB长度为10米)，另外三边用木栏围成，木栏总长20米，设动物场CD边的长为xm.

(1)、当矩形动物场面积为48m²时，求CD边的长；

(2)、能否围成面积为 $52 m^{2}$ 矩形动物场?说明理由.

查看试题解析
21. 已知：如图，四边形ABCD中， $∠ B A D = ∠ B C D$ $= 9 0^{°} ， E$ 为对角线BD的中点，点 $F$ 在边AD上，CF交BD于点 $G ， C F / / A E ， C F = \frac{1}{2} B D$ .

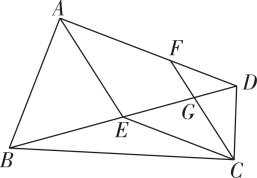(1)、求证：四边形AECF为菱形；

(2)、 $∠ D C G = ∠ D E C$ ，求证： $A E^{2} = A D \cdot D C$ .

查看试题解析

五、解答题(三)(本大题共2小题,每小题12分,共24分)

22. 直线 $y = x + b$ 与 $x$ 轴交于点 $C (4 ， 0)$ ，与 $y$ 轴交于点 $B$ ，并与双曲线 $y = \frac{m}{x} (x < 0)$ 交于点 $A (- 1 ， n)$ ，连接OA.

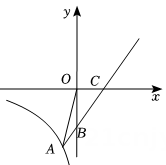(1)、求直线与双曲线的解析式.

(2)、在直线AC上存在一个点 $M$ (不与 $A$ 重合)，使得 $S_{△ O C M} = S_{△ A O C}$ ，求点 $M$ 的坐标.

(3)、若点 $D$ 在 $x$ 轴的正半轴上，是否存在以点D、C、B构成的三角形与 $△ O A B$ 相似?若存在求出 $D$ 点的坐标，若不存在，请说明理由.

查看试题解析
23. 某校数学活动小组在一次活动中，对一个数学问题作如下探究.

(1)、【问题发现】
如图①，在等边 $△ A B C$ 中，点 $P$ 是边BC上一点，且 $B P = \sqrt{7}$ ，连接AP，以AP为边作等边 $△ A P Q$ ，连接CQ.则CQ的长为；

(2)、【问题提出】
如图②，在等腰 $△ A B C$ 中， $A B = B C$ ，点 $P$ 是边BC上任意一点，以AP为腰作等腰 $△ A P Q$ ，使 $A P = P Q ， ∠ A P Q = ∠ A B C$ ，连接CQ.试说明 $∠ A B C$ 与 $∠ A C Q$ 相等；

(3)、【问题解决】
如图③，在正方形ADBC中，点 $P$ 是边BC上一点，以AP为边作正方形APEF，点 $Q$ 是正方形APEF的对称中心，连接CQ.若正方形APEF的边长为12， $C Q = 4 \sqrt{2}$ ，求正方形ADBC的边长.

查看试题解析