浙江省宁波市鄞州区2023-2024学年“迎春杯”七年级上学期数学能力测试卷
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题(每小题3分,共30分)
-
1. 下列各式运用等式的性质变形,正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则2. 下列说法:①在所有连结两点的线中,线段最短;②连接两点的线段叫做这两点的距离;③若线段 , 则点是线段AB的中点;④经过刨平的木板上的两个点,能弹出一条笔直的墨线,是因为两点确定一条直线,其中说法正确的是( )A、①②③ B、①②④ C、②③ D、①④3. 已知a,b是有理数,若a在数轴上的对应点的位置如图所示, , 有以下结论:①;②;③;④ , 则所有正确的结论是( )
 A、①④ B、①③ C、②③ D、②④4. 如图,线段 , C是上一点,且 , O是的中点,线段的长度是( )
A、①④ B、①③ C、②③ D、②④4. 如图,线段 , C是上一点,且 , O是的中点,线段的长度是( ) A、2cm B、3cm C、4cm D、5cm5. 如图,直线DE与BC相交于点与互余, , 则的度数是( )
A、2cm B、3cm C、4cm D、5cm5. 如图,直线DE与BC相交于点与互余, , 则的度数是( ) A、55 B、45 C、35 D、656. 我们知道实数和数轴上的点一 一对应,如图,正方形的边长为1,点是半圆与数轴的交点,则点对应的实数为( )
A、55 B、45 C、35 D、656. 我们知道实数和数轴上的点一 一对应,如图,正方形的边长为1,点是半圆与数轴的交点,则点对应的实数为( ) A、 B、 C、2.4 D、2.57. 要使多项式化简后不含的二次项,则的值是( )A、2 B、0 C、-2 D、-68. 满足的整数对(a,b)共有( )A、4个 B、5个 C、6个 D、7个9. 张阿姨准备在某商场购买一件衣服、一双鞋和一套化妆品,这三件物品的原价和优惠方式如下表所示.请帮张阿姨分析一下,选择一个最省钱的购买方案.此时,张阿姨购买这三件物品实际所付出的钱的总数为( )
A、 B、 C、2.4 D、2.57. 要使多项式化简后不含的二次项,则的值是( )A、2 B、0 C、-2 D、-68. 满足的整数对(a,b)共有( )A、4个 B、5个 C、6个 D、7个9. 张阿姨准备在某商场购买一件衣服、一双鞋和一套化妆品,这三件物品的原价和优惠方式如下表所示.请帮张阿姨分析一下,选择一个最省钱的购买方案.此时,张阿姨购买这三件物品实际所付出的钱的总数为( )欲购买的
商品
原价(元)
优惠方式
一件衣服
420
每付现金200元,返购物券200元,且付款时可以使用购物券
一双鞋
280
每付现金200元,返购物券200元,但付款时不可以使用购物券
一套化妆品
300
付款时可以使用购物券,但不返购物券
A、500元 B、600元 C、700元 D、800元10. 对于任意一个正整数xi可以按规则生成无穷数串:(其中为正整数),规则为:.下列说法:①若 , 则生成的这数串中必有(i为正整数);
②若 , 则;
③若生成的数中有一个 , 则它的前一个数应为32;
④若 , 则的值只能是9.
其中正确的个数是( )个
A、1 B、2 C、3 D、4二、填空题(每小题4分,共24分)
-
11. 4的平方根是12. 已知 , 比较这两个角的大小,结果为.(填“>”,“<”或“=”)13. 已知 , ,计算 的值为.14. 如图,在边长为9cm的正方形ABCD中,放置两张大小相同的正方形纸板,边EF在AB上,点K,I分别在BC,CD上,若区域Ⅰ的周长比区域Ⅱ与区域Ⅲ的周长之和还大6cm,则正方形纸板的边长为.
 15. 如图①,点在线段AB上,图中共有三条线段:线段AB,线段AC,线段CB,若其中有一条线段的长度是另一条线段长度的两倍,则称点为线段AB的“奇分点”.若 , 如图②,点从点开始以每秒3cm的速度向运动,当点到达点时停止运动,运动的时间为秒.当秒,是线段AB的“奇分点”(写出一种情况即可),如果同时点N从点的位置开始以每秒2cm的速度向点运动,如图③所示,并与点同时停止,则当秒,是线段AN的“奇分点”.
15. 如图①,点在线段AB上,图中共有三条线段:线段AB,线段AC,线段CB,若其中有一条线段的长度是另一条线段长度的两倍,则称点为线段AB的“奇分点”.若 , 如图②,点从点开始以每秒3cm的速度向运动,当点到达点时停止运动,运动的时间为秒.当秒,是线段AB的“奇分点”(写出一种情况即可),如果同时点N从点的位置开始以每秒2cm的速度向点运动,如图③所示,并与点同时停止,则当秒,是线段AN的“奇分点”. 16. 三个三位数由数字a,b组成,它们的和是2331,则的最大值是.
16. 三个三位数由数字a,b组成,它们的和是2331,则的最大值是.三、解答题(共46分)
-
17. 如图,点是线段AB的中点,点在上,且.
 (1)、若 , 求线段CD的长;(2)、CD=2,求线段AB的长.18. 美团外卖骑手分为专职和兼职两种,专职骑手月工资4000元保底,每送一单外卖可再得3元;兼职骑手没有保底工资,每送一单外卖可得4元。小张是一名专职美团骑手,小李是一名兼职美团骑手.(1)、若10月小张和小李送出的外卖单数相同,且小张比小李多收入了2500元,求小张送出了多少单外卖.(2)、根据国家个人所得税率标准,月工资超过5000时,需要交纳个人所得税,税率如下表所示:
(1)、若 , 求线段CD的长;(2)、CD=2,求线段AB的长.18. 美团外卖骑手分为专职和兼职两种,专职骑手月工资4000元保底,每送一单外卖可再得3元;兼职骑手没有保底工资,每送一单外卖可得4元。小张是一名专职美团骑手,小李是一名兼职美团骑手.(1)、若10月小张和小李送出的外卖单数相同,且小张比小李多收入了2500元,求小张送出了多少单外卖.(2)、根据国家个人所得税率标准,月工资超过5000时,需要交纳个人所得税,税率如下表所示:级数 工资范围 税率 1 不超过 5000 元 0% 2 超过 5000 至不超过 8000 的部分 3% 3 超过 8000 至不超过 17000 的部分 10% … … … 如果小张在11月交了200元的个人所得税,请问小张在11月送出了多少单外
19. 阅读与理解:对一个关于x的多项式求导数,多项式中xn的导数等于 , 常数项的导数为0.已知是关于的多项式,记为.我们规定:的导出多项式为 , 记为.例如:若 , 则的导出多项式;若 , 要求的导出多项式,先化简 , 则的导出多项式.根据以上材料,回答问题:(1)、若 , 则它的导出多项式.(2)、设是的导出多项式①若 , 求关于的方程的解;
②已知是关于的二次多项式,且关于的方程的解为整数,求正整数的值.
20. 如图1, 已知 ,射线 从 位置出发,以每秒 的速度按顺时针方向向射线 旋转;与此同时, 射线 以每秒 的速度,从 位置出发按逆时针方向向射线 旋转,到达射线 后又以同样的速度按顺时针方向返回,当射线 与射线 重合时,两条射线同时停止运动,设旋转时间为t(s).
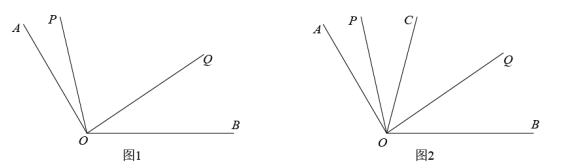 (1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.
(1)、当 时, 求 的度数;(2)、当 与 重合时,求 的值;(3)、如图2,在旋转过程中, 若射线 始终平分 ,问:是否存在 的值, 使得 若存在,请直接写出 的值;若不存在,请说明理由.