浙江省初中名校发展共同体2023-2024学年九年级第一学期数学中考模拟试卷
试卷更新日期:2024-02-02 类型:中考模拟
一、选择题(本题有10小题,每题3分,共30分。每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
-
1. 长城总长约为6700000米,用科学记数法表示是( )A、米 B、米 C、米 D、米2. 下列四个图形都是国际数学家大会的会标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算结果为的是( )A、 B、 C、 D、4. 实数在数轴上对应的点的位置如图所示,则a、-a、1的大小关系正确的是( )
3. 下列计算结果为的是( )A、 B、 C、 D、4. 实数在数轴上对应的点的位置如图所示,则a、-a、1的大小关系正确的是( )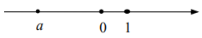 A、 B、 C、 D、5. 如图,直尺一边BC与量角器的零刻度线AD平行,已知的读数为 , 设OE与BC交于点 , 则的度数等于( )
A、 B、 C、 D、5. 如图,直尺一边BC与量角器的零刻度线AD平行,已知的读数为 , 设OE与BC交于点 , 则的度数等于( )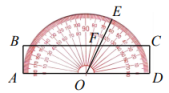 A、 B、 C、 D、6. 小明所在的班级有20人去体育场观看演出,20张票分别为区第10排1号到20号.采用随机抽取的办法分票,小明第一个抽取得到10号座位,接着小亮从其余的票中任意抽取一张,取得的一张恰与小明邻座的概率是( )A、 B、 C、 D、7. 如图,中,的外角平分线交射线BC于点 , 若 , 则的度数是( )
A、 B、 C、 D、6. 小明所在的班级有20人去体育场观看演出,20张票分别为区第10排1号到20号.采用随机抽取的办法分票,小明第一个抽取得到10号座位,接着小亮从其余的票中任意抽取一张,取得的一张恰与小明邻座的概率是( )A、 B、 C、 D、7. 如图,中,的外角平分线交射线BC于点 , 若 , 则的度数是( )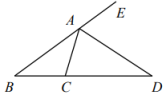 A、 B、 C、 D、8. 如图,已知点 , 点在双曲线上,点 , 点双曲线上,四边形ABCD为平行四边形.若轴,则平行四边形ABCD的面积等于( )
A、 B、 C、 D、8. 如图,已知点 , 点在双曲线上,点 , 点双曲线上,四边形ABCD为平行四边形.若轴,则平行四边形ABCD的面积等于( ) A、6 B、4 C、5 D、109. 如图是唐代李皋发明了“桨轮船”,该桨轮船的轮子被水面截得线段AB为10m,轮子的吃水深度3m,则该桨轮船的轮子直径为( )
A、6 B、4 C、5 D、109. 如图是唐代李皋发明了“桨轮船”,该桨轮船的轮子被水面截得线段AB为10m,轮子的吃水深度3m,则该桨轮船的轮子直径为( )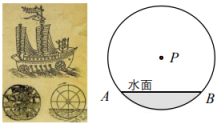 A、15m B、12m C、 D、10. 如图是由6块直角三角形拼成的矩形ABCD,其中①②③④是四个全等的三角形,则( )
A、15m B、12m C、 D、10. 如图是由6块直角三角形拼成的矩形ABCD,其中①②③④是四个全等的三角形,则( )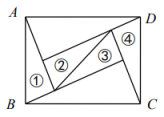 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每题4分,共24分)
-
11. 因式分解:.12. 某仓库对运进仓库的粮食采用如下的记录记法:运进120吨,记为+20吨;运进70吨记为-30吨.若运进90吨,则应记为吨.13. 设函数满足以下两个条件:①图象过点;②当时,随增大而增大.则满足条件的函数表达式可以是(写出一个即可).14. 如图,从笔直的公路旁一点出发,向西走3km到达 , 从出发向北走4km也到达.则从点向北偏西走到达.
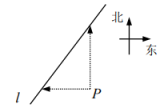 15. 如图,将边长为2的正五边形ABCDE沿对角线BE折叠,使点落在正五边形内部的处,则的长等于.
15. 如图,将边长为2的正五边形ABCDE沿对角线BE折叠,使点落在正五边形内部的处,则的长等于. 16. 有一种手持烟花,该烟花有10个花弹,每1秒发一发花弹,每一发花弹的飞行路径均相同.第一发花弹的飞行高度(米)与飞行时间(秒)满足关系式:.当秒时,该花弹的高度为米.(1)、第一发花弹的飞行高度的最大高度是米.(2)、第一发花弹飞行过程中与其他花弹同一高度时,其的值为.
16. 有一种手持烟花,该烟花有10个花弹,每1秒发一发花弹,每一发花弹的飞行路径均相同.第一发花弹的飞行高度(米)与飞行时间(秒)满足关系式:.当秒时,该花弹的高度为米.(1)、第一发花弹的飞行高度的最大高度是米.(2)、第一发花弹飞行过程中与其他花弹同一高度时,其的值为.三、解答题(本题有8小题,共66分)
-
17.(1)、计算:;(2)、解不等式:.18. 如图,在的正方形网格中,网格形成的最小边长的正方形的边长为1,点A,B在格点(网格线的交点)上.按要求画出格点四边形ABCD.
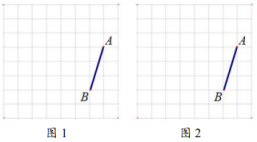 (1)、在图1中,画正方形ABCD.(2)、在图2中,画一个以AB为边的轴对称四边形ABCD(正方形除外).19. 甲、乙两校组织参加全市初中生英语口语竞赛,参赛人数相等.比赛成绩分别为7分、8分、9分、10分(满分为10分).依统计数据绘制了如下尚不完整的统计图表:
(1)、在图1中,画正方形ABCD.(2)、在图2中,画一个以AB为边的轴对称四边形ABCD(正方形除外).19. 甲、乙两校组织参加全市初中生英语口语竞赛,参赛人数相等.比赛成绩分别为7分、8分、9分、10分(满分为10分).依统计数据绘制了如下尚不完整的统计图表:
甲校成绩统计表分数 7分 8分 9分 10分 人数 11 0 m 8 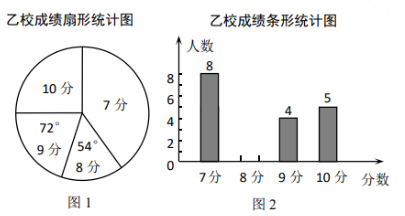 (1)、求甲校成绩统计表中m的值,并将图2的统计图补充完整.(2)、经计算,乙校的平均分是8.3分,中位数是8分,请求出甲校的平均分、中位数;并从平均分和中位数的角度分析两个学校成绩.20. 一个单位分数都可以写成两个单位分数的和:为正整数)(1)、若单位分数写成: , 求的值.(2)、设 , 即 , 试探究a,b与之间的关系,并写出推理过程.21. 已知关于的方程.(1)、试从等三个数中,选取一个数作为的值,使原方程有解,并说明理由,且求此解;(2)、当时,原方程有一根为 , 求的值。22. 如图,已知AB是的直径,弦于点 , 弦于点H,CF与AB交于点P,AF,CD的延长线交于点.连结AC,DF.
(1)、求甲校成绩统计表中m的值,并将图2的统计图补充完整.(2)、经计算,乙校的平均分是8.3分,中位数是8分,请求出甲校的平均分、中位数;并从平均分和中位数的角度分析两个学校成绩.20. 一个单位分数都可以写成两个单位分数的和:为正整数)(1)、若单位分数写成: , 求的值.(2)、设 , 即 , 试探究a,b与之间的关系,并写出推理过程.21. 已知关于的方程.(1)、试从等三个数中,选取一个数作为的值,使原方程有解,并说明理由,且求此解;(2)、当时,原方程有一根为 , 求的值。22. 如图,已知AB是的直径,弦于点 , 弦于点H,CF与AB交于点P,AF,CD的延长线交于点.连结AC,DF. (1)、求证:.(2)、若AC=3DF=3,求线段FH的长.23. 抛物线的顶点为.(1)、若 , 且抛物线过点 , 求抛物线的函数表达式;(2)、在(1)的条件下,直线与抛物线交于A、B两点,过A,B分别作轴的垂线,垂足为C,D,求的值.(3)、若直线与抛物线有两个交点,求的取值范围,并证明,两交点之间的距离与无关.24. 如图,边长为的正方形ABCD内部有一点(不在边界上),过点分别作两边的平行线EF,GH,与各边的交点分别为E,F,G,H,记四边形PHCF面积为 , 四边形PEAG的面积分别为 , 四边形PHBE的面积为 , 四边形PGDF的面积为.
(1)、求证:.(2)、若AC=3DF=3,求线段FH的长.23. 抛物线的顶点为.(1)、若 , 且抛物线过点 , 求抛物线的函数表达式;(2)、在(1)的条件下,直线与抛物线交于A、B两点,过A,B分别作轴的垂线,垂足为C,D,求的值.(3)、若直线与抛物线有两个交点,求的取值范围,并证明,两交点之间的距离与无关.24. 如图,边长为的正方形ABCD内部有一点(不在边界上),过点分别作两边的平行线EF,GH,与各边的交点分别为E,F,G,H,记四边形PHCF面积为 , 四边形PEAG的面积分别为 , 四边形PHBE的面积为 , 四边形PGDF的面积为.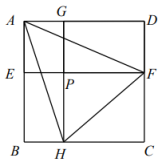 (1)、若 , 求的值;(2)、若 , 求证:;(3)、对于确定的值,试讨论在线段EF上存在几点 , 使得.
(1)、若 , 求的值;(2)、若 , 求证:;(3)、对于确定的值,试讨论在线段EF上存在几点 , 使得.