浙江省杭州市拱墅区2023-2024学年九年级上学期数学期末模拟卷
试卷更新日期:2024-02-02 类型:期末考试
一、选择题(本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
-
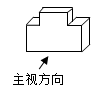
1. 一个布袋里放着4个黑球和2个白球,它们除了颜色以外没有任何其他区别.把布袋中的球搅匀后,从中任取3个球,则下列事件中属于必然事件的是( )A、3个都是黑球 B、2个黑球1个白球 C、2个白球1个黑球 D、至少有1个黑球2. 某服务台如图所示,它的主视图为( )
 A、
A、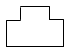 B、
B、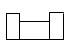 C、
C、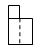 D、
D、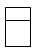 3. 将y=﹣(x+4)2+1的图象向右平移2个单位,再向下平移3个单位,所得函数最大值为( )A、y=﹣2 B、y=2 C、y=﹣3 D、y=34. ⊙O的半径为7,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定5. 若2y﹣5x=0,则x:y等于( )A、2:5 B、4:25 C、5:2 D、25:46. 在 中, , , ,那么下列结论正确的是( )A、 B、 C、 D、7. 若分式不论x取任何数总有意义,则m的取值范围是( )A、 B、 C、 D、8. 如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为( )
3. 将y=﹣(x+4)2+1的图象向右平移2个单位,再向下平移3个单位,所得函数最大值为( )A、y=﹣2 B、y=2 C、y=﹣3 D、y=34. ⊙O的半径为7,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定5. 若2y﹣5x=0,则x:y等于( )A、2:5 B、4:25 C、5:2 D、25:46. 在 中, , , ,那么下列结论正确的是( )A、 B、 C、 D、7. 若分式不论x取任何数总有意义,则m的取值范围是( )A、 B、 C、 D、8. 如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为( )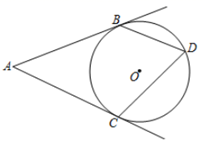 A、130° B、65° C、50°或130° D、65°或115°9. 如图,在⊙O中,直径MN=10,正方形ABCD的四个顶点都分别在半径OP、OM及⊙O上,且∠POM=45°,则AB=( )
A、130° B、65° C、50°或130° D、65°或115°9. 如图,在⊙O中,直径MN=10,正方形ABCD的四个顶点都分别在半径OP、OM及⊙O上,且∠POM=45°,则AB=( ) A、2 B、 C、 D、310. 将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )A、 B、 C、或 D、或
A、2 B、 C、 D、310. 将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )A、 B、 C、或 D、或二、填空题(本大题有6个小题,每小题4分,共30分)
-
11. 在平面直角坐标系xOy中,已知点A的坐标为(2,3),那么直线OA与x轴夹角的正切值是 .12. 一根内径为3cm的圆柱形长试管中装满了水,现把试管中的水逐渐滴入一个内径为8cm、高为1.8cm的圆柱形玻璃杯中,当玻璃杯装满水时,试管中的水的高度下降了cm.13. ⊙O的半径为2,弦BC=2 , 点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .14. 如图,在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为、、.若抛物线的图象与正方形ABCD有公共点,则a的取值范围是.
 15. 不透明袋中有红、白两种颜色的小球,这些球除颜色外无其他差别.从袋中随机取出一个球是红球的概率是0.6,若袋中有4个白球,则袋中红球有个.16. 如图,⊙O的半径为10,点P在⊙O上,点A在⊙O内,且AP=6,过点A作AP的垂线交QO于点B,C.若PC=15,则PB=.
15. 不透明袋中有红、白两种颜色的小球,这些球除颜色外无其他差别.从袋中随机取出一个球是红球的概率是0.6,若袋中有4个白球,则袋中红球有个.16. 如图,⊙O的半径为10,点P在⊙O上,点A在⊙O内,且AP=6,过点A作AP的垂线交QO于点B,C.若PC=15,则PB=.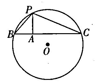
三、解答题(本大题有7小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
17. 计算:.18. 有 张看上去无差别的卡片,上面分别写着 ,随机抽取 张后,放回并混在一起,再随机抽取 张.
(1)、请用树状图或列表法等方法列出各种可能出现的结果;(2)、求两次抽到的卡片上的数字之和等于 的概率.19. 已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M. (1)、求证:△ABF≌△DAE;(2)、求证:△AMF∽△ADE;(3)、观察判断BF与AE有怎样的位置关系?20. 暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
(1)、求证:△ABF≌△DAE;(2)、求证:△AMF∽△ADE;(3)、观察判断BF与AE有怎样的位置关系?20. 暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:甲
乙
进价(元/部)
4000
2500
售价(元/部)
4300
3000
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)、若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?(2)、通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.21. 风力发电是指把风的动能转为电能.风能是一种清洁无公害的可再生能源,利用风力发电非常环保,且风能蕴量巨大,因此风力发电日益受到我们国家的重视.某校学生开展综合实践活动,测量风力发电扇叶轴心的高度.如图,已知测倾器的高度为1.6m,在测点A处安置测倾器,测得扇叶轴心点M的仰角 , 再与点A相距3.5m的测点B处安置测倾器,测得点M的仰角(点A,B与N在一条直线上)求扇叶轴心离地面的高度的长.(精确到1m;参考数据: , , )

