广东省深圳市福田区重点学校2023-2024学年九年级上学期12月月考数学试卷

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列四种图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一个正方体截去四分之一，得到如图所示的几何体，其左视图是（　　）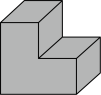

A、 B、 C、 D、

查看试题解析
3. 因深圳市委正紧紧围绕打造“志愿者之城”4.0升级版，推动志愿服务事业朝着更专业、更精细、更规范的方向不断迈进，截至2022年底，深圳市注册志愿者已达3510000人，平均每5个深圳市民里就有一个志愿者．其中数据3510000用科学记数法表示为（　　）

A、3.51×10⁵ B、3.51×10⁶ C、3.51×10⁷ D、0.351×10⁷

查看试题解析
4. 下列计算中，结果正确的是（　　）

A、（－pq）³＝p³q³ B、x·x³＋x²·x²＝x⁸ C、 $\sqrt{25}$ ＝±5 D、（a²）³＝a⁶

查看试题解析
5. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如表所示．
成绩/米
1.50
1.60
1.65
1.70
1.75
人数
2
3
5
4
1
这些运动员成绩的众数和中位数分别为（　　）

A、1.65米，1.65米 B、1.65米，1.70米 C、1.75米，1.65米 D、1.50米，1.60米

查看试题解析
6. 解不等式组 ${\begin{array}{l} 7 x - 8 < 9 x ① \\ \frac{x + 1}{2} ⩽ x ② \end{array}$ 时，不等式①②的解集在同一条数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
7. 小华将一副三角板（∠C＝∠D＝90°，∠B＝30°，∠E＝45°）按如图所示的方式摆放，其中AB∥EF，则∠1的度数为（　　）

A、45° B、60° C、75° D、105°

查看试题解析
8. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木条，绳子还余4.5尺；将绳子对折再量木条，木条余1尺，问木条长多少尺？若设木条长x尺，绳子长y尺，则可列方程组为（　　）

A、 ${\begin{array}{l} y = x + 4.5 \\ 0.5 y = x - 1 \end{array}$ B、 ${\begin{array}{l} y = x - 4.5 \\ 0.5 y = x + 1 \end{array}$
${\begin{array}{l} y = x + 4.5 \\ y = 2 x - 1 \end{array}$
${\begin{array}{l} y = x - 4.5 \\ y = 2 x - 1 \end{array}$

查看试题解析
9. 如图，把一张矩形纸片ABCD按所示方法进行两次折叠，得到等腰直角三角形BEF，若BC＝1，则AB的长度为（　　）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2} + 1}{2}$ C、 $\frac{\sqrt{5} + 1}{2}$ D、 $\frac{4}{3}$

查看试题解析
10. 如图，正方形ABCD的边长为4，点E，F分别在边DC，BC上，且BF＝CE，AE平分∠CAD，连接DF，分别交AE，AC于点G，M．P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM．有下列四个结论：
①AE垂直平分DM；②PM＋PN的最小值为3 $\sqrt{2}$ ；③CF²＝GE•AE；④S_△_ADM＝6 $\sqrt{2}$ ．
其中正确的是（　　）

A、①② B、②③④ C、①③④ D、①③

查看试题解析

二、填空题（每题3分，共15分）

11. 分解因式： $2 a^{2} + 8 a b + 8 b^{2} =$ ．

查看试题解析
12. 若二次根式 $\frac{1}{\sqrt{2 - x}}$ 有意义，则x的取值范围是.

查看试题解析
13. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问：径几何？”转化为现在的数学语言表达就是：如图，CD为⊙O的直径，弦AB⊥CD，垂足为E，CE＝1寸，AB＝10寸，则直径CD的长度为寸．

查看试题解析
14. 如图，在△ABC中，D是边AB上一点，按以下步骤作图：
①以点A为圆心，以适当长为半径作弧，分别交AB，AC于点M，N；
②以点D为圆心，以AM长为半径作弧，交DB于点M^'；
③以点M^'为圆心，以MN长为半径作弧，在∠BAC内部交前面的弧于点N^'；
④过点N^'作射线DN^'交BC于点E．
若△BDE与四边形ACED的面积比为4：21，则 $\frac{B E}{C E}$ 的值为．

查看试题解析
15. 如图，在△ABC中，∠ACB＝90°，AC＝8，将△ABC绕点C按逆时针方向旋转得到△A₁B₁C，满足A₁B₁∥AC，过点B作BE⊥A₁C，垂足为E，连接AE，若S_△_ABE＝3S_△_ACE ，则AB的长为．

查看试题解析

三、解答题（共55分）

16. 计算： $\sqrt{16} - 2 t a n 6 0^{°} - {(\frac{1}{2})}^{- 1} + (π - 2023)^{0}$ ．

查看试题解析
17. 先化简，再求值： $(\frac{1}{x - 1} - x + 1) \div \frac{x - 2}{x^{2} - 1}$ ，其中 $x = \sqrt{2}$

查看试题解析
18. 某校为落实“双减”工作，推行“五育并举”，计划成立五个兴趣活动小组（每个学生只能参加一个活动小组）：A．音乐，B．美术，C．体育，D．阅读，E．人工智能．为了解学生对以上兴趣活动的参与情况，随机抽取了部分学生进行调查统计，并根据统计结果，绘制成了如图所示的两幅不完整的统计图：
根据图中信息，完成下列问题：

(1)、①补全条形统计图（要求在条形图上方注明人数）；
②扇形统计图中的圆心角α的度数为 ▲ ．

(2)、若该校有3600名学生，估计该校参加E组（人工智能）的学生人数；

(3)、该学校从E组中挑选出了表现最好的两名男生和两名女生，计划从这四位同学中随机抽取两人参加市青少年人工智能竞赛，请用画树状图或列表的方法求出恰好抽到一名男生一名女生的概率．

查看试题解析
19. 随着国家乡村振兴政策的推进，凤凰村农副产品越来越丰富．为增加该村村民收入，计划定价销售某土特产，他们把该土特产（每袋成本10元）进行4天试销售，日销量y（袋）和每袋售价x（元）记录如下：
时间
第一天
第二天
第三天
第四天
x/元
15
20
25
30
y/袋
25
20
15
10
若试销售和正常销售期间，日销量y与每袋售价x的一次函数关系相同，解决下列问题：

(1)、求日销量y关于每袋售价x的函数关系式；

(2)、请你帮村民设计，每袋售价定为多少元，才能使这种土特产每日销售的利润最大？并求出最大利润．（利润＝销售额－成本）

查看试题解析
20. 如图， $△ A B C$ 中，以 $A B$ 为直径的 $⊙ O$ 交 $B C$ 于点E． $A E$ 平分 $∠ B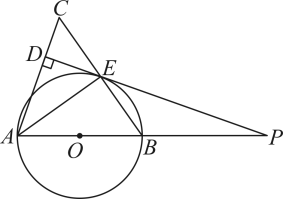 A C$ ，过点E作 $E D ⊥ A C$ 于点D，延长 $D E$ 交 $A B$ 的延长线于点P．

(1)、求证： $P E$ 是 $⊙ O$ 的切线；

(2)、若 $s i n ∠ P = \frac{1}{3} ， B P = 4$ ，求 $C D$ 的长．

查看试题解析

21. 视力表中蕴含着很多数学知识，如：每个“

”形图都是正方形结构，同一行的“

”是全等图形且对应着同一个视力值，不同的检测距离需要不同的视力表．

素材1 国际通用的视力表以5米为检测距离，任选视力表中7个视力值n，测得对应行的“”形图边长b（mm），在平面直角坐标系中描点如图1．

探究1 检测距离为5米时，归纳n与b的关系式，并求视力值1.2所对应行的“”形图边长．

素材2 图2为视网膜成像示意图，在检测视力时，眼睛能看清最小“”形图所成的角叫做分辨视角θ．视力值n与分辨视角θ（分）的对应关系近似满足n＝ $\frac{1}{θ}$ （0.5≤θ≤10）．

探究2 当n≥1.0时，属于正常视力，根据函数增减性写出对应的分辨视角θ的范围．

素材3 如图3，当θ确定时，在A处用边长为b₁的Ⅰ号“”测得的视力与在B处用边长为b₂的Ⅱ号“”测得的视力相同．

探究3 若检测距离为3米，求视力值1.2所对应行的“”形图边长．

查看试题解析

22. 过四边形 $A B C D$ 的顶点A作射线 $A M$ ， P为射线 $A M$ 上一点，连接 $D P$ ．将 $A P$ 绕点A顺时针方向旋转至 $A Q$ ，记旋转角 $∠ P A Q = α$ ，连接 $B Q$ ．

(1)、【探究发现】如图1，数学兴趣小组探究发现，如果四边形 $A B C D$ 是正方形，且 $α = 90 °$ ．无论点P在何处，总有 $B Q = D P$ ，请证明这个结论．

(2)、【类比迁移】如图2，如果四边形 $A B C D$ 是菱形， $∠ D A B = α = 60 °$ ， $∠ M A D = 15 °$ ，连接 $P Q$ ．当 $P Q ⊥ B Q$ ， $A B = \sqrt{6} + \sqrt{2}$ 时，求 $A P$ 的长；

(3)、【拓展应用】如图3，如果四边形 $A B C D$ 是矩形， $A D = 6$ ， $A B = 8$ ， $A M$ 平分 $∠ D A C$ ， $α = 90 °$ ．在射线 $A Q$ 上截取 $A R$ ，使得 $A R = \frac{4}{3} A P$ ．当 $△ P B R$ 是直角三角形时，请直接写出 $A P$ 的长．

查看试题解析

时间	第一天	第二天	第三天	第四天
x/元	15	20	25	30
y/袋	25	20	15	10

成绩/米	1.50	1.60	1.65	1.70	1.75
人数	2	3	5	4	1