广东省深圳市南山区重点学校2023-2024学年上学期八年级12月月考数学试卷

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 可以用来说明命题“若a²＝b² ，则a＝b”是假命题的反例是（）

A、a＝4，b＝5 B、a＝4，b＝4 C、a＝4，b＝－4 D、a＝4，b＝－5

查看试题解析
2. 若x轴上的点P到y轴的距离为3，则点P为（）

A、（3，0） B、（3，0）或（－3，0） C、（0，3） D、（0，3）或（0，－3）

查看试题解析
3. 实数a在数轴上的位置如图所示，则 $\sqrt{{(a - 4)}^{2}} + \sqrt{{(a - 11)}^{2}}$ 化简后为（）

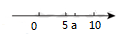A、7 B、-7 C、2a-15 D、无法确定

查看试题解析
4. 为响应我市申请创建文明城市，我校举行了“创建文明城市应知应会知识”的知识竞赛，某班的学生成绩统计如下表，则该班学生成绩的众数和平均数分别是（）
成绩（分）
60
70
80
90
100
人数
2
8
17
10
3

A、70分，80分 B、80分，81分 C、90分，80分 D、80分，79分

查看试题解析
5. 如图，正方形ABCD的顶点A，B的坐标分别为（1，1），（3，1），若正方形ABCD第1次沿x轴翻折，第2次沿y轴翻折，第3次沿x轴翻折，第4次沿y轴翻折，第5次沿x轴翻折，…则第2021次翻折后点C对应点的坐标为（）

A、（3，－3） B、（3，3） C、（－3，3） D、（－3，－3）

查看试题解析
6. 如图，网格中的每个小正方形的边长为1， $△ A B C$ 的顶点 $A$ ， $B$ ， $C$ 均在网格的格点上， $B D ⊥ A C$ 于点 $D$ ，则 $B D$ 的长为（）

A、 $\frac{2}{3} \sqrt{5}$ B、 $\frac{3}{4} \sqrt{5}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\frac{3}{5} \sqrt{5}$

查看试题解析
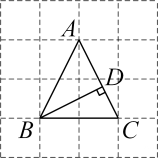7. 把直线y＝－5x沿着y轴平移后得到直线AB，直线AB经过点（a，b），且5a＋b＝－2．则直线AB的函数表达式是（）

A、y＝－5x＋2 B、y＝－5x－2 C、y＝5x＋2 D、y＝5x－2

查看试题解析
8. 甲、乙两人同时分别从A，B两地同向匀速行走，他们与A地的距离S（km）与所行的时间t（h）之间的函数关系如图中的函数图象，则当他们行了3h的时候，他们之间的距离是（）

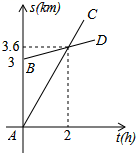A、1km B、1.5km C、2km D、2.5km

查看试题解析
9. 对于任意实数x，x均能写成其整数部分[x]与小数部分{x}的和，即x＝[x]＋{x}，其中[x]称为x的整数部分，表示不超过x的最大整数，{x}称为x的小数部分．比如1.3＝[1.3]＋{1.3}＝1＋0.3，[1.3]＝1，{1.3}＝0.3，－1.3＝[－1.3]＋{－1.3}＝－2＋0.7，[－1.3]＝－2，{－1.3}＝0.7则下列结论正确的有（）
①{－0.4}＝－0.4；
②若x＋y＝n是整数，则[x]＋[y]＝n或n－1；
③若[x]＝1，[y]＝2，[z]＝3，则[x＋y＋z]所有可能的值为6，7，8；
④方程3x－{x}＝2[x]＋3的解为x＝3；
⑤[x]＋[x＋0.5]＝[2x]对一切实数x均成立．

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如图，在△ABC中，∠ACB＝90°，以AC，BC和AB为边向上作正方形ACEF和正方形BCMI和正方形ABGF，点G落在MI上，若AC＋BC＝7，空白部分面积为16，则图中阴影部分的面积是（）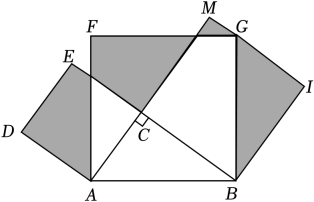

A、16 B、15 C、 $\frac{66}{5}$ . D、 $\frac{99}{5}$

查看试题解析

二、填空题（每题3分，共15分）

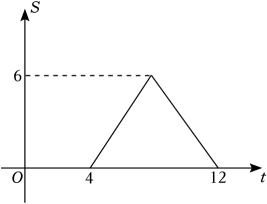
11. 计算 $\sqrt{3 a} \cdot \sqrt{12 a b}$ （a≥0，b≥0）＝．

查看试题解析
12. 在社团剪纸活动中，小罗同学将剪好的窗花放在适当的平面直角坐标系内，点A（3，n）与点B（m，2）恰好关于x轴对称，则mⁿ的值为．

查看试题解析
13. 已知x＝1－a，且y＝1－3a，用x的代数式表示y为．（化为最简形式）

查看试题解析
14. 小明参加“传承经典，筑梦未来”主题演讲比赛，其演讲形象、演讲内容、演讲效果三项成绩分别是9分、8分、9分．若将演讲形象、演讲内容、演讲效果三项成绩按2：5：3确定最终成绩，则小明的最终比赛成绩是分．

查看试题解析
15. 已知△ABC，动点P从点A出发，以每秒钟1个单位长度的速度沿A→B→C→A方向运动到点A处停止，设点P运动的时间为t秒，△PAB的面积S关于t的函数图象如图所示，则△ABC的边BC上的高等于．

查看试题解析

三、解答题（共55分）

16. 计算：

(1)、2 $\sqrt{2}$ －| $\sqrt{2}$ －1|；

(2)、 $\sqrt{0.04} + \sqrt[3]{- 8} - \sqrt{\frac{1}{4}}$ ．

查看试题解析
17. 解方程组 ${\begin{cases} \frac{x ＋ y}{3} ＋ \frac{x － y}{2} ＝ 1 \\ 2 (x ＋ y) － 3 x ＋ 3 y ＝ 6 \end{cases}$ ．

查看试题解析
18. 如图所示，△ABC在正方形网格中，若点A的坐标为（0，3），按要求回答下列问题：

(1)、在图中建立正确的平面直角坐标系；

(2)、作出△ABC关于x轴的对称图形△A'B'C'；（不用写作法）

(3)、求△A'B'C'的面积．

查看试题解析
19. 某学校调查九年级学生对“二十大”知识的了解情况，进行了“二十大”知识竞赛测试，从两班各随机抽取了10名学生的成绩，整理如下：（成绩得分用x表示，共分成四组：A.80≤x＜85，B.85≤x＜90，C.90≤x＜95，D.95≤x≤100）
九年级（1）班10名学生的成绩是：96，80，96，86，99，98，92，100，89，82．
九年级（2）班10名学生的成绩在C组中的数据是：94，90，92．
通过数据分析，列表如下：
年级
平均数
中位数
众数
方差
九年级（1）班
91.8
b
c
52
九年级（2）班
92
93
100
50.4
九年级（1）班、（2）班抽取的学生竞赛成绩统计表
根据以上信息，解答下列问题：

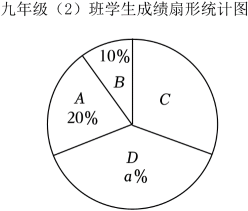(1)、直接写出上述a、b、c的值：a＝， b＝， c＝；

(2)、学校欲选派成绩更稳定的班级参加下一阶段的活动，根据表格中的数据，学校会选派哪一个班级？说明理由．

(3)、九年级两个班共120人参加了此次调查活动，估计两班参加此次调查活动成绩优秀（x≥90）的学生总人数是多少？

查看试题解析
20. 冰墩墩（BingDuenDuen）是2022年北京冬季奥运会的吉祥物．将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员．在冬奥会期间，冰墩墩玩偶持续畅销．小冬从某进货渠道购进A，B两款冰墩墩玩偶共30个，在自家商店销售．两款玩偶的进货价和销售价如表：
价格类别
A款玩偶
B款玩偶
进货价（元/个）
20
15
销售价（元/个）
28
20
设A款玩偶购进x个，获利y元．

(1)、求出y（元）与x（个）之间的函数表达式；

(2)、进货渠道规定A款玩偶进货数量不得超过B款玩偶进货数量的一半．小冬应如何设计进货方案才能获得最大利润，最大利润是多少？

查看试题解析
21. 已知一个三位自然数m，若满足十位数字等于百位数字与个位数字之和，则称这个数为“平衡数”，并把其百位数字与个位数字的乘积记为F（m）．
例如693，∵3＋6＝9，∴693是“平衡数”．F（693）＝6×3＝18．
规定：G（m，n）＝sF（m）＋tF（n）（s，t均为非零实数，m，n均为平衡数）．
已知：G（253，121）＝5，G（231，693）＝－16．

(1)、求s，t及G（286，341）的值；

(2)、已知“平衡数”m个位数为7，同时与“平衡数”n满足G（m，n）＝ $\sqrt{F (m) - 10}$ ，求n的所有可能值；

(3)、已知m，n是两个十位数字相同的“平衡数”，m加上其各个数位上数字之和是7的倍数，若G（m，n）＝－5，求n的所有可能值．

查看试题解析
22. 【阅读材料】说明代数式 $\sqrt{x^{2} + 1} + \sqrt{(x - 3)^{2} + 4}$ 的几何意义，并求它的最小值．
解： $\sqrt{x^{2} + 1} + \sqrt{(x - 3)^{2} + 4} = \sqrt{(x - 0)^{2} + (0 - 1)^{2}} + \sqrt{(x - 3)^{2} + (0 - 2)^{2}}$ ，如图1，建立平面直角坐标系，点P（x，0）是x轴上一点，则 $\sqrt{(x - 0)^{2} + (0 - 1)^{2}}$ 可以看成点P与点A（0，1）的距离， $\sqrt{(x - 3)^{2} + (0 - 2)^{2}}$ 可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是求PA＋PB的最小值．
设点A关于x轴的对称点为A′，则PA＝PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短，所以PA′＋PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C＝3，CB＝3，所以 $A^{^{'}} B = 3 \sqrt{2}$ ，即原式的最小值为 $3 \sqrt{2}$ ．
根据以上阅读材料，解答下列问题：

(1)、【基础训练】代数式 $\sqrt{(x - 1)^{2} + 1} + \sqrt{(x - 3) + 16}$ 的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B 的距离之和；（填写点B的坐标）

(2)、【能力提升】求代数式 $\sqrt{x^{2} + 49} + \sqrt{x^{2} - 12 x + 37}$ 的最小值为；

(3)、【拓展升华】如图2，在等腰直角△ABC中，∠BAC＝90°，点M，N分别为BC，AC上的动点，且 $A N = C M ， A B = \sqrt{2}$ ．当AM＋BN的值最小时，求CM的长．

查看试题解析

年级	平均数	中位数	众数	方差
九年级（1）班	91.8	b	c	52
九年级（2）班	92	93	100	50.4

价格类别	A款玩偶	B款玩偶
进货价（元/个）	20	15
销售价（元/个）	28	20

成绩（分）	60	70	80	90	100
人数	2	8	17	10	3