广东省深圳市罗湖区2023-2024学年八年级上学期数学期末模考试题
试卷更新日期:2024-02-02 类型:期末考试
一、选择题(本部分共10小题,每小题3分,共30分)
-
1. 下列四个实数中,为无理数的是( )A、0 B、 C、 D、2. 如图,已知直线 , 把三角板的直角顶点放在直线b上.若 , 则的度数为( )
 A、140° B、130° C、120° D、110°3. 在平面直角坐标系中,点 的坐标是 ,点 与点 关于 轴对称,则点 的坐标是( )A、 B、 C、 D、4. 在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是( )
A、140° B、130° C、120° D、110°3. 在平面直角坐标系中,点 的坐标是 ,点 与点 关于 轴对称,则点 的坐标是( )A、 B、 C、 D、4. 在“经典诵读”比赛活动中,某校10名学生参赛成绩如图所示,对于这10名学生的参赛成绩,下列说法正确的是( )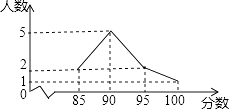 A、众数是90分 B、中位数是95分 C、平均数是95分 D、方差是155. 若函数(k为常数,且)中,y随x的增大而增大,则其图像可能是( )A、
A、众数是90分 B、中位数是95分 C、平均数是95分 D、方差是155. 若函数(k为常数,且)中,y随x的增大而增大,则其图像可能是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D , 交AB于E , 若CD=3,则AD等于( )
6. 如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D , 交AB于E , 若CD=3,则AD等于( ) A、12 B、10 C、8 D、67. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )
A、12 B、10 C、8 D、67. 如图,为了测算出学校旗杆的高度,小明将升旗的绳子拉到旗杆底端,并在与旗杆等长的地方打了一个结,然后将绳子底端拉到离旗杆底端5米的地面某处,发现此时绳子底端距离打结处约1米,则旗杆的高度是( )
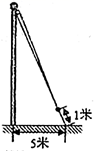 A、12 B、13 C、15 D、248. 如图,在中, , 平分 , 垂直平分 , 若 , 则的值为( )
A、12 B、13 C、15 D、248. 如图,在中, , 平分 , 垂直平分 , 若 , 则的值为( ) A、 B、 C、1 D、9. 如图,用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形,则每个小长方形的周长是( )
A、 B、 C、1 D、9. 如图,用12块形状和大小均相同的小长方形纸片拼成一个宽是60厘米的大长方形,则每个小长方形的周长是( )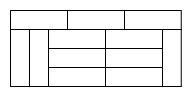 A、60厘米 B、80厘米 C、100厘米 D、120厘米10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
A、60厘米 B、80厘米 C、100厘米 D、120厘米10. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距千米;
②乙车比甲车晚出发小时,却早到小时;
③乙车出发后小时追上甲车;
④当甲、乙两车相距千米时,或
其中正确的结论有( )
 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(本部分共5小题,每小题3分,共15分).
-
11. 16的算术平方根是12. 若点 , 都在一次函数的图象上,则 . (填“”或“”)13. 已知关于x、y的二元一次方程组的解是 , 则一次函数和的图像交点坐标为 .14. 如图,在Rt△ABC中,∠ABC=90°,DE是AC的垂直平分线,交AC于点D,交BC于点E,若∠C=35°,则∠BAE= .
 15. A , B两地相距20km , 甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.
15. A , B两地相距20km , 甲从A地出发向B地前进,乙从B地出发向A地前进,两人沿同一直线同时出发,甲先以8km/h的速度前进1小时,然后减慢速度继续匀速前进,甲乙两人离A地的距离s(km)与时间t(h)的关系如图所示,则甲出发小时后与乙相遇.
三、解答题(本大题共7题.其中16题6分,17题7分,18题7分,19题8分,20题8分,21题10分,22题9分,共55分).
-
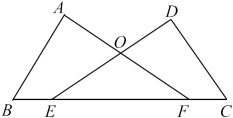
16. 计算:(1)、 .(2)、17. 解下列方程(1)、;(2)、 .18. 如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O , 且AB=DC , BE=CF .
求证:∠B=∠C .
 19. 在第二十二届深圳读书月来临之际,为了解某学校八年级学生每天平均课外阅读时间的情况,随机抽查了该学校八年级部分同学,对其每天平均课外阅读时间进行统计,并绘制了如图所示的不完整的统计图.请根据相关信息,解答下列问题:
19. 在第二十二届深圳读书月来临之际,为了解某学校八年级学生每天平均课外阅读时间的情况,随机抽查了该学校八年级部分同学,对其每天平均课外阅读时间进行统计,并绘制了如图所示的不完整的统计图.请根据相关信息,解答下列问题: (1)、该校抽查八年级学生的人数为 , 图中的 值为 ;(2)、请将条形统计图补充完整;(3)、求被抽查的学生每天平均课外阅读时间的众数、中位数和平均数;(4)、根据统计的样本数据,估计该校八年级400名学生中,每天平均课外阅读时间为2小时的学生有多少人?20. 为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买 、 两种不同型号的篮球共300个.已知购买3个 型篮球和2个 型篮球共需340元,购买2个 型篮球和1个 型篮球共需要210元.(1)、求购买一个 型篮球、一个 型篮球各需多少元?(2)、若该校计划投入资金 元用于购买这两种篮球,设购进的 型篮球为 个,求 关于 的函数关系式;(3)、学校在体育用品专卖店购买 、 两种型号篮球共300个,经协商,专卖店给出如下优惠: 种球每个降价8元, 种球打9折,计算下来,学校共付费16740元,学校购买 、 两种篮球各多少个?
(1)、该校抽查八年级学生的人数为 , 图中的 值为 ;(2)、请将条形统计图补充完整;(3)、求被抽查的学生每天平均课外阅读时间的众数、中位数和平均数;(4)、根据统计的样本数据,估计该校八年级400名学生中,每天平均课外阅读时间为2小时的学生有多少人?20. 为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买 、 两种不同型号的篮球共300个.已知购买3个 型篮球和2个 型篮球共需340元,购买2个 型篮球和1个 型篮球共需要210元.(1)、求购买一个 型篮球、一个 型篮球各需多少元?(2)、若该校计划投入资金 元用于购买这两种篮球,设购进的 型篮球为 个,求 关于 的函数关系式;(3)、学校在体育用品专卖店购买 、 两种型号篮球共300个,经协商,专卖店给出如下优惠: 种球每个降价8元, 种球打9折,计算下来,学校共付费16740元,学校购买 、 两种篮球各多少个?

