广东省惠州市惠东重点学校 2023-2024学年九年上学期级数学期末模拟卷
试卷更新日期:2024-02-02 类型:期末考试
一、单选题(每小题3分,共30分)
-
1. 下列标志图中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中,是一元二次方程的是( )A、X3+2x=0 B、X(x-3)=0 C、 D、y-x2=43. 已知关于x的一元二次方程(1-m)x2+2x-2=0有两个不相等的实数根,则m的取值范围是( )A、m< B、m> C、m≤且m≠1 D、m<且m≠14. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、通过抛掷一枚均匀的硬币确定谁先发球的比赛规则是不公平的 C、“垂直于弦的直径平分这条弦”是不确定事件 D、“367人中至少有2人生日相同”是必然事件5. 把抛物线y=(x-2)2+3先向左平移3个单位长度,再向下平移5个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(-1,2) B、(1,-2) C、(-1,-2) D、(1,2)6. 如图,内接于⊙ , 连接 , 则( )
2. 下列方程中,是一元二次方程的是( )A、X3+2x=0 B、X(x-3)=0 C、 D、y-x2=43. 已知关于x的一元二次方程(1-m)x2+2x-2=0有两个不相等的实数根,则m的取值范围是( )A、m< B、m> C、m≤且m≠1 D、m<且m≠14. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、通过抛掷一枚均匀的硬币确定谁先发球的比赛规则是不公平的 C、“垂直于弦的直径平分这条弦”是不确定事件 D、“367人中至少有2人生日相同”是必然事件5. 把抛物线y=(x-2)2+3先向左平移3个单位长度,再向下平移5个单位长度,则经过这两次平移后所得抛物线的顶点坐标是( )A、(-1,2) B、(1,-2) C、(-1,-2) D、(1,2)6. 如图,内接于⊙ , 连接 , 则( )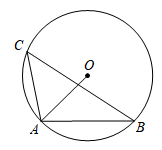 A、 B、 C、 D、7. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )
A、 B、 C、 D、7. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )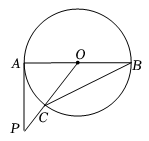 A、25° B、35° C、40° D、50°8. 有一个正n边形旋转90°后与自身重合,则n为( )A、6 B、9 C、12 D、159. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=8 cm,AB=6 cm.动点E从点C开始沿边CB向终点B以2 cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1 cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
A、25° B、35° C、40° D、50°8. 有一个正n边形旋转90°后与自身重合,则n为( )A、6 B、9 C、12 D、159. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,AD=8 cm,AB=6 cm.动点E从点C开始沿边CB向终点B以2 cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1 cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )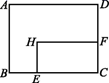 A、
A、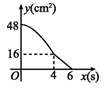 B、
B、 C、
C、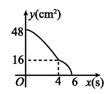 D、
D、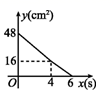
二、填空题(每小题3分,共15分)
-
11. 已知点A(﹣2,b)与点B(a,3)关于原点对称,则a﹣b =.12. 已知x1 , x2是一元二次方程x2-4x+3=0的两根,则x1+x2-x1x2= .13. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是 .
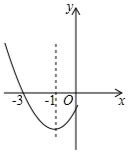 14. 若圆锥的母线长为 , 其侧面积为 , 则圆锥底面半径为 .15. 如图,等边△ABC中,AB=3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为 .
14. 若圆锥的母线长为 , 其侧面积为 , 则圆锥底面半径为 .15. 如图,等边△ABC中,AB=3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为 .
三、解答题(16-18每题8分共24分,19-21每题9分共27分,22-23每题12分共24分)
-
16. 用适当的方法解方程:(1)、.(2)、.17. 如图,某小区矩形绿地的长宽分别为35m,15m.现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地.
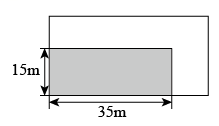 (1)、若扩充后的矩形绿地面积为 , 求新的矩形绿地的长与宽;(2)、扩充后,实地测量发现新的矩形绿地的长宽之比为 . 求新的矩形绿地面积.18. 在平面直角坐标系中的位置如图所示。
(1)、若扩充后的矩形绿地面积为 , 求新的矩形绿地的长与宽;(2)、扩充后,实地测量发现新的矩形绿地的长宽之比为 . 求新的矩形绿地面积.18. 在平面直角坐标系中的位置如图所示。 (1)、把向上平移5个单位后得到对应的 , 请画出;(2)、以原点O为对称中心,画出与关于原点O对称的 , 并写出点的坐标.19. 今年6月份,永州市某中学开展“六城同创”知识竞赛活动.赛后,随机抽取了部分参赛学生的成绩,按得分划为A,B,C,D四个等级,A:,B:,C:,D:.并绘制了如图两幅不完整的统计图,请结合图中所给信息,解答下列问题:
(1)、把向上平移5个单位后得到对应的 , 请画出;(2)、以原点O为对称中心,画出与关于原点O对称的 , 并写出点的坐标.19. 今年6月份,永州市某中学开展“六城同创”知识竞赛活动.赛后,随机抽取了部分参赛学生的成绩,按得分划为A,B,C,D四个等级,A:,B:,C:,D:.并绘制了如图两幅不完整的统计图,请结合图中所给信息,解答下列问题: (1)、请把条形统计图补充完整.(2)、扇形统计图中 , , B等级所占扇形的圆心角度数为 .(3)、对甲、乙、丙、丁4名参加知识竞赛学生进行分组作业调查,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)20. 某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件.(1)、求销售价在每件90元的基础上,每件降价多少元时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠?(2)、要想平均每天盈利2000元,可能吗?请说明理由.21. 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)、请把条形统计图补充完整.(2)、扇形统计图中 , , B等级所占扇形的圆心角度数为 .(3)、对甲、乙、丙、丁4名参加知识竞赛学生进行分组作业调查,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)20. 某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件.(1)、求销售价在每件90元的基础上,每件降价多少元时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠?(2)、要想平均每天盈利2000元,可能吗?请说明理由.21. 如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.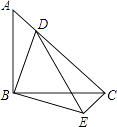 (1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.22. 图1是某型号汤碗,截面如图2所示,碗体部分为半圆O , 直径 , 倒汤时, , 如图3所示.
(1)、求∠DCE的度数;(2)、若AB=4,CD=3AD,求DE的长.22. 图1是某型号汤碗,截面如图2所示,碗体部分为半圆O , 直径 , 倒汤时, , 如图3所示. (1)、的度数为;(2)、在图3中,通过计算比较直径与的长度哪个更长;(3)、请在图3中画出线段 , 用其长度表示汤(阴影部分)的最大深度(不说理由),并求汤的最大深度.23. 如图,在平面直角坐标系中,抛物线与直线交于点 , .
(1)、的度数为;(2)、在图3中,通过计算比较直径与的长度哪个更长;(3)、请在图3中画出线段 , 用其长度表示汤(阴影部分)的最大深度(不说理由),并求汤的最大深度.23. 如图,在平面直角坐标系中,抛物线与直线交于点 , .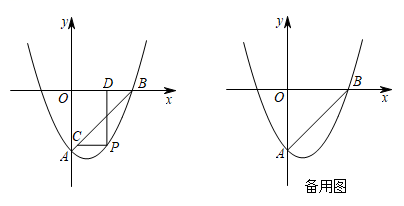 (1)、求该抛物线的函数表达式;(2)、点是直线下方拋物线上的一动点,过点作轴的平行线交于点 , 过点作轴的平行线交轴于点 , 求的最大值及此时点的坐标;(3)、在(2)中取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点 , 使得以点 , , , 为顶点的四边形是平行四边形,写出所有符合条件的点的坐标,并写出求解点的坐标的其中一种情况的过程.
(1)、求该抛物线的函数表达式;(2)、点是直线下方拋物线上的一动点,过点作轴的平行线交于点 , 过点作轴的平行线交轴于点 , 求的最大值及此时点的坐标;(3)、在(2)中取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点为点的对应点,平移后的抛物线与轴交于点 , 为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点 , 使得以点 , , , 为顶点的四边形是平行四边形,写出所有符合条件的点的坐标,并写出求解点的坐标的其中一种情况的过程.