湖北省曾都区2023-2024学年七年级上学期数学期中考试试题

试卷更新日期：2024-02-02 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题2分，共20分）

1. ﹣2的倒数等于（）

A、1 B、 $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ D、﹣2

查看试题解析
2. 下列各数：﹣π，﹣|﹣2|，2022，﹣1.010010001，﹣3.5中，负数的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列各式中，不相等的是（　　）

A、（﹣3）²和﹣3² B、（﹣3）²和3² C、（﹣2）³和﹣2³ D、|﹣2|³和|﹣2³|

查看试题解析
4. 手机支付给生活带来便捷，如图是王老师某日微信账单的收支明细（正数表示收入，负数表示支出，单位：元），王老师当天微信收支的最终结果是（）

A、收入14元 B、支出3元 C、支出18元 D、支出10元

查看试题解析
5. 下列说法中错误的有（）
①﹣1与0之间没有负数；②如果|x|＝2，那么x的值是2；③两个数比较大小绝对值大的反而小； ④如果x＝﹣x，那么x＝0；⑤如果|x|＝x，那么x＝0； ⑥如果两个数的和为0，那么这两个数互为相反数．

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 下列结论中正确的是（）

A、单项式 $\frac{π x y^{2}}{4}$ 的系数是 $\frac{1}{4}$ ，次数是4 B、单项式m的次数是1，没有系数 C、多项式2x²+xy²+3是二次三项式 D、2x+y，﹣a²b，0它们都是整式

查看试题解析
7. 用四舍五入法，分别按要求取2.1704的近似值，下列结果错误的是（　　）

A、2.2（精确到0.1） B、2.17（精确到0.01） C、2（精确到个位） D、2.17（精确到千分位）

查看试题解析
8. 下列关于方程的变形，正确的是（）

A、由3+x＝7，得x＝7+3 B、由5x＝﹣4，得x＝﹣ $\frac{5}{4}$ C、由 $\frac{7}{4}$ x＝3得x＝3× $\frac{7}{4}$ D、由﹣ $\frac{x - 2}{4}$ ＝1，得﹣（x﹣2）＝4

查看试题解析
9. 若xy＝x﹣2，则2xy+3x﹣5xy+10的值为（）

A、4 B、10 C、16 D、20

查看试题解析
10. 任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数0. $\overset{•}{7}$ 为例进行说明：设 $0 . \overset{•}{7} = x$ ，由 $0 . \overset{•}{7} = 0.7777 …$ 可知，10x＝7.777⋯⋯ ，所以10x﹣x＝7，解方程，得x＝ $\frac{7}{9}$ ．于是，得 $0 . \overset{•}{7} = \frac{7}{9}$ ，将 $0 . \overset{•}{3} \overset{•}{6}$ 写成分数的形式是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{11}$ D、 $\frac{5}{11}$

查看试题解析

二、填空题（共14小题，每小题2分，共28分）

11. 若代数式3a+1的值与代数式3（a﹣1）的值互为相反数，则a＝；

查看试题解析
12. 将数据15.7万用科学记数法表示为；

查看试题解析
13. 大于﹣4.6而小于2.3的整数共有个；

查看试题解析
14. 多项式 $\frac{1}{5} x^{2} y^{|m|} - (m + 1) y + \frac{1}{7}$ 是关于x，y的三次二项式，则m的值是；

查看试题解析
15. 近似数1.70的准确值a的取值范围是；

查看试题解析
16. 若单项式7x¹^﹣^my²ⁿ和﹣4x³y⁴是同类项，则mⁿ的值为．

查看试题解析
17. 若方程（m²﹣1）x²﹣（m-1）x+2＝0是关于x的一元一次方程，则代数式|m﹣1|的值为；

查看试题解析
18. 当x＝2023时，代数式ax³+bx+5的值为1，则当x＝﹣2023时，ax³+bx+5的值为．

查看试题解析
19. 已知|a|＝3，|b﹣1|＝5，且a＞b，则a+b的值为；

查看试题解析
20. 已知a、b、c在数轴上位置如图，则|a+b|+|a+c|﹣|b﹣c|=

查看试题解析
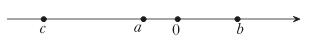21. 已知a，b为有理数，下列结论：①若a＞b，则 $\frac{1}{a} < \frac{1}{b}$ ； ②若a+b＝0，则 $\frac{a}{b} = 1$ ；③若a³+b³＝0，则a+b＝0； ④|a|＝|﹣2|，则a＝﹣2； ⑤若ab＞0，则|a+b|＝|a|+|b|； ⑥ a²≥a．
其中正确的为．（填序号）

查看试题解析
22. 定义一个运算f（a，b）＝ ${\begin{array}{l} a + b (a < b) \\ a - b (a > b) \end{array}$ ，已知|a﹣2|＝1，b＝2，那么f（a，b）＝．

查看试题解析
23. 若|m﹣2023|与|2022﹣n|互为相反数，则 $\frac{2}{(m - 1) (n - 1)} + \frac{2}{(m - 2) (n - 2)} + ⋯ + \frac{2}{(m - 2021) (n - 2021)}$ 的值为．

查看试题解析
24. 如图，由一块正方形地和一块长方形地组成的花园，分别以正方形的边长为半径画圆弧，以长方形的长为直径画圆弧，如图所示．园艺师准备在阴影部分种花，则阴影部分的种植面积为平方米？（用含a的代数式表示，结果保留π）．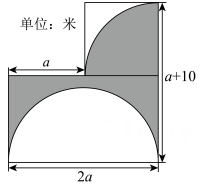

查看试题解析

三、解答题（共8小题，共72分）

25. 计算：

(1)、﹣23+36﹣（﹣27）﹣40×2；

(2)、﹣1⁴﹣（1﹣0.5）× $\frac{1}{3}$ [3﹣（﹣3）²]；

查看试题解析
26. 先化简，再求值：
2a²b﹣[2ab²﹣2（ $\frac{1}{2}$ ab﹣ $\frac{3}{2}$ a²b﹣1）+ab]+2ab²+2，其中a＝﹣3，b＝2；

查看试题解析
27. 解方程：

(1)、5x+3＝﹣2x﹣11；

(2)、3（y﹣7）﹣5（4﹣y）＝15；

查看试题解析
28. 乐乐在妈妈的监督下进行了7次跳绳检测，检测他一分钟跳绳的个数，并把每次的个数都与前一次进行比较，超出的部分记为“+”，不足的部分记为“﹣”．下表记录了他第2次到第7次的检测结果．
第2次
第3次
第4次
第5次
第6次
第7次
+1
﹣8
+5
+4
+5
n

(1)、若乐乐第1次的检测成绩为m个．请直接写出：
①第4次检测成绩的个数（用m表示）
②第2次到第6次的检测中成绩超过m个的次数．

(2)、若乐乐第1次的检测成绩为100个，第7次的检测成绩为106个．
①求表中n的值；
②乐乐妈妈为了鼓励乐乐，每跳绳一个奖励1颗小星星，并从第2次开始，与前一次进行比较，每超过一个再额外奖励2颗小星星，求乐乐这7次检测共能得到多少颗小星星．

查看试题解析
29. 如图为武汉市地铁2号线地图的一部分，学生小王某天参加志愿者服务活动，从洪山广场站出发，到从A站出站时，本次志愿者服务活动结束．如果规定向东为正，向西为负，当天的乘车站数按先后顺序依次记录如下：+4，﹣3，+6，﹣8，+5，﹣2，﹣3，+1．

(1)、请通过计算说明A站是哪一站？

(2)、若相邻两站之间的平均距离为1.2千米，求这次小王志愿服务期间乘坐地铁行进的总路程约是多少千米？

查看试题解析
30. 已知代数式A＝2x²﹣2x﹣1，B＝﹣x²+xy+1，M＝4A﹣（3A﹣2B）．

(1)、当（x+1）²+|y﹣2|＝0时，求代数式M的值．

(2)、若代数式（2x²+ax﹣y+6）﹣（2bx²﹣3x+5y﹣1）的值与字母x的取值无关，求代数式2A﹣B的值．

查看试题解析
31. 已知a是最大的负整数，b是-5的相反数，且a、b分别是点A、B、在数轴上对应的数．

(1)、求a、b的值，并在数轴上标出点A、B．

(2)、若动点P从点A出发沿数轴正方向运动，动点Q同时从点B出发也沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，若运动t秒后，点P可以追上点Q，求t的值？

查看试题解析
32. 观察下面有一定规律的三组数：（1）﹣2，4，﹣6，8，﹣10，…；（2）﹣5，1，﹣9，5，﹣13，…；（3） $\frac{1}{2}$ ， ﹣1， $\frac{3}{2}$ ， ﹣2， $\frac{5}{2}$ ， …；
解答下列问题：

(1)、每组的第7个数分别是，，；

(2)、第二组和第三组的第n个数分别是，；（用含n的式子来表示）

(3)、取每组的第k个数，若这三个数的和为172，求k的值．

查看试题解析

第2次	第3次	第4次	第5次	第6次	第7次
+1	﹣8	+5	+4	+5	n