浙江省杭州市萧山城区六校2023-2024学年七年级上学期12月独立作业数学试题

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、选择题：本题有10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的．

1. 杭州第19届亚运会开幕式现场直播及相关报道，中央广播电视总台全媒体多平台的跨媒体总阅读播放量达到 $5.03$ 亿次， $503000000$ 用科学记数法表示为（）

A、 $5.03 \times 1 0^{9}$ B、 $5.03 \times 1 0^{8}$ C、 $0.503 \times 1 0^{9}$ D、 $50.3 \times 1 0^{7}$

查看试题解析
2. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数，用正、负数来表示只有相反意义的量．一次数学测试，以80分为基准简记，90分记作+10分，那么70分应记作（）

A、+10分 B、0分 C、－10分 D、－20分

查看试题解析
3. 64的平方根是（）

A、 4 B、±4 C、8 D、±8

查看试题解析
4. 已知 $- 25 a^{2 m} b$ 和 $7 a^{4} b^{3 - n}$ 是同类项，则 $3 m - 2 n$ 的值是（）

A、6 B、4 C、3 D、2

查看试题解析
5. 如图，下列说法错误的是（）

A、直线 $A C$ 还可以表示为直线 $C A$ 或直线m B、射线 $A C$ 与射线 $C A$ 不是同一条射线 C、点B在直线m上 D、图中有直线1条，射线4条，线段1条

查看试题解析
6. 下列变形中正确的是（）

A、若 $x = y$ ，则 $x + a = y - a$ B、若 $\frac{x}{m} = \frac{y}{m}$ ，则 $x = y$ C、若 $\frac{x + 1}{2} - 3 = \frac{x}{3}$ ，则 $x + 1 - 3 = 2 x$ D、若 $x = y$ ，则 $\frac{x}{m} = \frac{y}{m}$

查看试题解析
7. 下列说法正确的是（）

A、 $\frac{1}{x} + 1$ 是多项式 B、 $\frac{3 x + y}{3}$ 是单项式 C、 $- m n^{5}$ 是五次单项式 D、 $- x^{2} y - 2 x^{3} y$ 是四次多项式

查看试题解析
8. 《九章算术》中有这样一个问题：“今有共买物，人出八，盈三；人出七，不足四；问人数几何？”大意为：若干人共同出资购买某物品，若每人出八钱，则多了三钱；若每人出七钱，则少了四钱，问共有几人？设人数共有 $x$ 人，则可列方程为（）

A、 $8 x - 3 = 7 x + 4$ B、 $8 x + 3 = 7 x - 4$ C、 $8 x + 4 = 7 x - 3$ D、 $8 x - 4 = 7 x + 3$

查看试题解析
9. 下列说法正确的是（）
①若 $x = 1$ 是关于x的方程 $a + b x + c = 0$ 的一个解，则 $a + b + c = 0$ ；②在等式 $3 x = 3 a - b$ 两边都除以3，可得 $x = a - b$ ；③若 $b = 2 a$ ，则关于x的方程 $a x + b = 0 (a \neq 0)$ 的解为 $x = - \frac{1}{2}$ ；④在等式 $a = b$ 两边都除以 $x^{2} + 1$ ，可得 $\frac{a}{x^{2} + 1} = \frac{b}{x^{2} + 1}$ ．

A、①③ B、②④ C、①④ D、②③

查看试题解析
10. 有理数a，b在数轴上对应的位置如图所示，那么代数式 $\frac{| a + 1 |}{a + 1} - \frac{| a |}{a} + \frac{b - a}{| a - b |} - \frac{1 - b}{| b - 1 |}$ 的值是（）

A、﹣1 B、0 C、1 D、2

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分．

11. $- π$ 的相反数是，绝对值是．

查看试题解析
12. 萧山区2023年中考考生人数四舍五入取近似值后约有 $1.3$ 万人，那么这个数值是精确到位．

查看试题解析
13. 若 $x = 1$ 是关于x的方程 $\frac{a - x}{2} = \frac{1}{2} - a + 2 x$ 的解，则 $a =$ ．

查看试题解析
14. 观察下列算式：① $3^{2} - 1^{2} = 8$ ， ② $5^{2} - 3^{2} = 16$ ， ③ $7^{2} - 5^{2} = 24$ ， ④ $9^{2} - 7^{2} = 32$ ， …，请用你发现的规律将第n个式子表示出来：．

查看试题解析
15. 七年级某班同学，每人都会游泳或滑冰，其中会游泳的人数比会滑冰的人数多10人，两种都会的有5人，设只会滑冰的有 $a$ 人，则该班同学共有（用含 $a$ 的代数式表示）人．

查看试题解析
16. 已知M是满足不等式 $- \sqrt{2} < a < \sqrt{7}$ 的所有整数的和，N是 $\sqrt{52}$ 的整数部分，则 $M + N$ 的平方根为．

查看试题解析

三、解答题：本题有8小题，共66分．解答应写出文字说明或推演步骤．

17. 计算：

(1)、 $(- 15) - (- 23) + (- 17) + 5$ ；

(2)、 $- 2^{3} + \frac{1}{3} \times [- 9 + {(- 3)}^{2}]$ ．

查看试题解析
18. 解方程：

(1)、 $2 (x - 1) = 2 - 5 (x + 2)$

(2)、 $\frac{5 x + 1}{2} - \frac{7 x + 2}{4} = 1$

查看试题解析
19. 化简：

(1)、 $5 a - (2 a - 4 b)$ ；

(2)、 $2 x^{2} + 3 (2 x - x^{2})$ ．

查看试题解析
20. 如图，已知线段AB ，点C在AB上，点P在AB外．

(1)、根据要求画出图形：画直线PA ，画射线PB ，连接PC；

(2)、写出图中的所有线段．

查看试题解析
21. 求值：

(1)、已知 $5 x - 2 y = 3$ ，求 $15 x - 6 y - 8$ 的值.

(2)、已知 $a - b = 5 ， - a b = 3$ ，求 $(7 a + 4 b + a b) - 6 (\frac{5}{6} b + a - a b)$ 的值.

查看试题解析
22. 为抗击新冠肺炎疫情，某药店对消毒液和口罩开展优惠活动.已知消毒液每瓶定价比口罩每包定价多5元，按照定价售出4包口置和3瓶消毒液共需要43元.

(1)、求一包口罩和一瓶消毒液定价各多少元？

(2)、优惠方案有以下两种：
方案一：以定价购买时，买一瓶消毒液送一包口罩；方案二：消毒液和口罩都按定价的九折付款.

现某客户要到该药店购买消毒液20瓶，口罩x包（x>20）.

①若客户购买150包口罩时，请通过计算说明哪种方案购买较为省钱？

②求当客户购买多少包口罩时，两种方案的购买总费用一样.

查看试题解析
23. 如图，把图（1）中两个小正方形纸片分别沿对角线剪开，将所得的4个直角三角形拼在一起，就得到如图（2）的大正方形．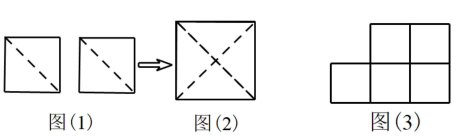

(1)、问题发现：若大正方形的面积为 $32 c m^{2}$ ，则小正方形的面积是 $c m^{2}$ ，边长为 $c m$ ；

(2)、拓展延伸：如图（3）是由5个边长为1的小正方形组成的纸片，能否把它剪开并拼成一个大正方形？若能，请画出示意图，并写出边的长度，若不能，请说明理由．

查看试题解析
24. 已知数轴上点A表示的数为 $- 5$ ，点B是数轴上在点A右侧的一点，且A、B两点间的距离为8个单位长度，点P为数轴上的一个动点，其对应的数为x ．

(1)、写出点B所表示的数为．

(2)、①若点P到点A ，点B的距离相等，则点P所表示的数为．
②数轴上是否存在点P ，使点P到点A ，点B的距离之和为10，若存在，求出x的值，若不存在，说明理由．

(3)、点A以1个单位长度/秒向右运动，点B以2个单位长度/秒的速度向左运动，同时点P以5个单位长度/秒从原点向左运动，当点P遇到点A时，立即以原来的速度向右运动，当点P遇到点B时，立即以原来的速度向左运动，并不停地往返于点A与点B之间，求当点A与点B重合时点P所经过的总路程，并直接写出此时点P在数轴上表示的数．

查看试题解析