黑龙江省鸡西市2023-2024学年上学期第二次质量监测九年级数学试题
试卷更新日期:2024-02-02 类型:月考试卷
一、选择题(每题3分,满分30分)
-
1. 下列式子是一元二次方程的是( )A、x2﹣2x﹣3 B、x2+1=y C、5﹣x(x﹣1)=5 D、2x﹣1=02. 下列各曲线是根据不同的函数绘制而成的,其中是中心对称图形的是( )A、
 B、
B、 C、
C、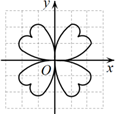 D、
D、 3. 下列事件中,属于必然事件的是( )A、抛掷硬币时,正面朝上 B、13人中至少有2人的生日在同一月份 C、经过红绿灯路口,遇到红灯 D、玩“石头、剪刀、布”游戏时,对方出“剪刀”4. 把抛物线 y=3x2 先向上平移2个单位,再向右平移3个单位,所得抛物线的表达式是( )A、y=3(x+3)2﹣2 B、y=3(x+2)2+3 C、y=3(x﹣3)2﹣2 D、y=3(x﹣3)2+25. 如图,在⊙O中,弦AB,CD相交于点P,若∠A=50°,∠APD=82°,则∠B的大小是( )
3. 下列事件中,属于必然事件的是( )A、抛掷硬币时,正面朝上 B、13人中至少有2人的生日在同一月份 C、经过红绿灯路口,遇到红灯 D、玩“石头、剪刀、布”游戏时,对方出“剪刀”4. 把抛物线 y=3x2 先向上平移2个单位,再向右平移3个单位,所得抛物线的表达式是( )A、y=3(x+3)2﹣2 B、y=3(x+2)2+3 C、y=3(x﹣3)2﹣2 D、y=3(x﹣3)2+25. 如图,在⊙O中,弦AB,CD相交于点P,若∠A=50°,∠APD=82°,则∠B的大小是( )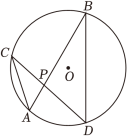 A、32° B、42° C、48° D、52°6. 电影《长津湖》讲述了一段波澜壮阔的历史,一上映就获得全国人民的追捧.已知第一天票房约为2亿元,前三天票房累计约10亿元.若每天票房的增长率都为x,依题意可列方程为( )A、2(1+x)=10 B、2(1+x)2=10 C、2+2(1+x)2=10 D、2+2(1+x)+2(1+x)2=107. 如图,将△OAB绕着点O逆时针旋转至△OA′B′,使点B恰好落在线段A′B′上,若∠AOA′=32°,则∠B′的度数为( )
A、32° B、42° C、48° D、52°6. 电影《长津湖》讲述了一段波澜壮阔的历史,一上映就获得全国人民的追捧.已知第一天票房约为2亿元,前三天票房累计约10亿元.若每天票房的增长率都为x,依题意可列方程为( )A、2(1+x)=10 B、2(1+x)2=10 C、2+2(1+x)2=10 D、2+2(1+x)+2(1+x)2=107. 如图,将△OAB绕着点O逆时针旋转至△OA′B′,使点B恰好落在线段A′B′上,若∠AOA′=32°,则∠B′的度数为( ) A、 B、 C、 D、8. 习近平总书记强调:“青年一代有理想、有本领、有担当,国家就有前途,民族就有希望”.如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心, , 长分别为半径,圆心角形成的扇面,若 , , 则阴影部分的面积为( )
A、 B、 C、 D、8. 习近平总书记强调:“青年一代有理想、有本领、有担当,国家就有前途,民族就有希望”.如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心, , 长分别为半径,圆心角形成的扇面,若 , , 则阴影部分的面积为( )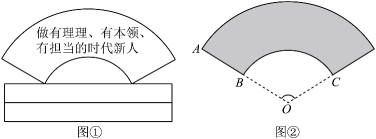 A、 B、 C、 D、9. 如图,在一张Rt△ABC纸片中,∠ACB=90°,BC=5,AC=12,⊙O是它的内切圆.小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE,则△ADE的周长为( )
A、 B、 C、 D、9. 如图,在一张Rt△ABC纸片中,∠ACB=90°,BC=5,AC=12,⊙O是它的内切圆.小明用剪刀沿着⊙O的切线DE剪下一块三角形ADE,则△ADE的周长为( ) A、19 B、17 C、22 D、2010. 如图,在正方形ABCD中,M,N分别是AB,CD的中点,P是线段MN上的一点,BP的延长线交AD于点E,连接PD,PC,将△DEP绕点P顺时针旋转90°得△GFP,则下列结论:①CP=GP;②∠CGF=45°;③BC垂直平分FG;④若AB=4,点E在AD边上运动,则D,F两点之间距离的最小值是 . 其中结论正确的序号有( )
A、19 B、17 C、22 D、2010. 如图,在正方形ABCD中,M,N分别是AB,CD的中点,P是线段MN上的一点,BP的延长线交AD于点E,连接PD,PC,将△DEP绕点P顺时针旋转90°得△GFP,则下列结论:①CP=GP;②∠CGF=45°;③BC垂直平分FG;④若AB=4,点E在AD边上运动,则D,F两点之间距离的最小值是 . 其中结论正确的序号有( ) A、②③ B、①②③ C、①②④ D、①③④
A、②③ B、①②③ C、①②④ D、①③④二、填空题(每题3分,满分30分)
-
11. 若点与点关于原点对称,则的值为 .12. 已知点 A(-4,y1) , B(-1,y2),C(5,y3) 三点在抛物线上,则 , , 的大小关系是为 (用“<”连接).13. 已知关于x的一元二次方程(k﹣1)x2+2x+1=0有实数根,则k的取值范围是.14. 杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2m,拱高(桥拱圆弧的中点到弦的距离)约为2m,则此桥拱的半径是.
 15. 一个不透明的袋子中装有若干个白球和3个黄球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黄球的频率稳定在左右,则袋子中白球约有个.16. 如图,冰激凌蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是.
15. 一个不透明的袋子中装有若干个白球和3个黄球,这些球除颜色外均相同.经多次摸球试验后发现,摸到黄球的频率稳定在左右,则袋子中白球约有个.16. 如图,冰激凌蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是.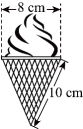 17. 已知一元二次方程x2﹣3x+1=0的两根分别为m,n,则﹣m﹣n﹣mn的值是.18. 如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 .
17. 已知一元二次方程x2﹣3x+1=0的两根分别为m,n,则﹣m﹣n﹣mn的值是.18. 如图,⊙O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=10,则⊙O的面积为 . 19. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=6,点D在BC边上,将点A绕点D顺时针旋转90°得到点E,连接DE,CE.当△DCE是等腰三角形时,BD的长为 .
19. 如图,在Rt△ABC中,∠B=90°,AB=4,BC=6,点D在BC边上,将点A绕点D顺时针旋转90°得到点E,连接DE,CE.当△DCE是等腰三角形时,BD的长为 . 20. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A( , 0),B(0,2),则点A2023的坐标是 .
20. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A( , 0),B(0,2),则点A2023的坐标是 .
三、解答题(共60分)
-
21. 解方程:(1)、(2)、22. 如图,在正方形网格中,每个小正方形的边长均为1个单位长度,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣1,2),B(﹣3,1),C(0,﹣1).
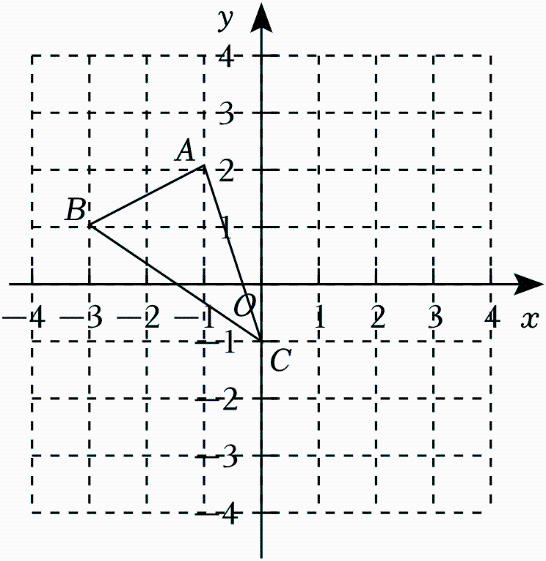 (1)、将△ABC向右平移2个单位长度得到 △A'B'C' ,画出 △A'B'C' ;(2)、将△ABC绕点C按顺时针方向旋转90°后得到△ , 画出△;(3)、在(2)的条件下,求边AC扫过的面积.23. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校以中国传统节日端午节为契机,组织全体学生参加包粽子劳动体验活动,随机调查了部分学生,对他们每个人平均包一个粽子的时长进行统计,并根据统计结果绘制成如下不完整的统计图表.
(1)、将△ABC向右平移2个单位长度得到 △A'B'C' ,画出 △A'B'C' ;(2)、将△ABC绕点C按顺时针方向旋转90°后得到△ , 画出△;(3)、在(2)的条件下,求边AC扫过的面积.23. 2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校以中国传统节日端午节为契机,组织全体学生参加包粽子劳动体验活动,随机调查了部分学生,对他们每个人平均包一个粽子的时长进行统计,并根据统计结果绘制成如下不完整的统计图表.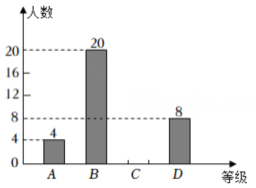
根据图表信息,解答下列问题:(1)、本次调查的学生为 人,表中x的值为 ;(2)、该校共有500名学生,请你估计等级为B的学生人数;(3)、本次调查中,等级为A的4人中有两名男生和两名女生,若从中随机抽取两人进行活动感想交流,请利用画树状图或列表的方法,求恰好抽到一名男生和一名女生的概率.等级
时长t(单位:分钟)
人数
所占百分比
A
0≤t<2
4
x
B
2≤t<4
20
C
4≤t<6
36%
D
t≥6
16%
24. 随着“双减”政策落地,周末家庭野外郊游将成为我们的生活常态.小双骑自行车从家里出发30分钟后到达甲地,游玩一段时间后按原速前往乙地.小双离家1小时30分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程与小双离家时间的函数图象,已知妈妈驾车的速度是小双骑车速度的3倍,根据图中的信息: (1)、小双从家出发多少小时后被妈妈追上?此时离家多远?(2)、若妈妈比小双还早10分钟到达乙地,从家到乙地的路程是多少?25. 问题情境:数学课上,老师引导同学们以“正方形中线段的旋转”为主题开展数学活动.已知正方形中, , 点E是射线上一点(不与点C重合),连接 , 将绕点E顺时针旋转得到 , 连接 .
(1)、小双从家出发多少小时后被妈妈追上?此时离家多远?(2)、若妈妈比小双还早10分钟到达乙地,从家到乙地的路程是多少?25. 问题情境:数学课上,老师引导同学们以“正方形中线段的旋转”为主题开展数学活动.已知正方形中, , 点E是射线上一点(不与点C重合),连接 , 将绕点E顺时针旋转得到 , 连接 .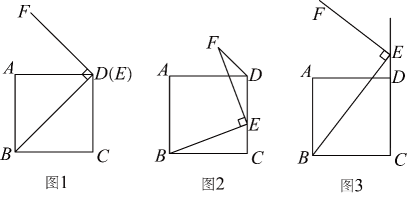 (1)、特例分析:如图1,当点E与点D重合时,则=;(2)、深入谈及:当点E不与点D重合时,(1)中的结论是否仍然成立?若成立,请在图2与图3中选择一种情况进行证明;若不成立,请说明理由;26. 社区利用一块矩形空地建了一个小型停车场,其布局如图所示.已知 , , 阴影部分设计为停车位,要铺花砖,其余部分均为宽度为米的道路.已知铺花砖的面积为 .
(1)、特例分析:如图1,当点E与点D重合时,则=;(2)、深入谈及:当点E不与点D重合时,(1)中的结论是否仍然成立?若成立,请在图2与图3中选择一种情况进行证明;若不成立,请说明理由;26. 社区利用一块矩形空地建了一个小型停车场,其布局如图所示.已知 , , 阴影部分设计为停车位,要铺花砖,其余部分均为宽度为米的道路.已知铺花砖的面积为 . (1)、求道路的宽是多少米?(2)、该停车场共有车位个,据调查分析,当每个车位的月租金为元时;可全部租出;若每个车位的月租金每上涨元,就会少租出个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为元。27. 抛物线与x轴交于点 , 与y轴交于点C.
(1)、求道路的宽是多少米?(2)、该停车场共有车位个,据调查分析,当每个车位的月租金为元时;可全部租出;若每个车位的月租金每上涨元,就会少租出个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为元。27. 抛物线与x轴交于点 , 与y轴交于点C. (1)、求抛物线的解析式(2)、在抛物线对称轴上找一点M,使△MBC的周长最小,并求出点M的坐标和△MBC的周长(3)、若点P是x轴上的一个动点,过点P作交抛物线于点Q,在抛物线上是否存在点Q,使B、C、P、Q为顶点的四边形为平行四边形?若存在请直接写出点Q的坐标,若不存在请说明理由.
(1)、求抛物线的解析式(2)、在抛物线对称轴上找一点M,使△MBC的周长最小,并求出点M的坐标和△MBC的周长(3)、若点P是x轴上的一个动点,过点P作交抛物线于点Q,在抛物线上是否存在点Q,使B、C、P、Q为顶点的四边形为平行四边形?若存在请直接写出点Q的坐标,若不存在请说明理由.