广东省佛山市南海区桂城街道2023-2024学年八年级（上）期中数学试卷
试卷更新日期：2024-02-02 类型：期中考试
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项正确）
-
1. 下列四个数中，无理数是（ ）A、 B、2 C、0 D、﹣1.52. 25的算术平方根是（ ）A、5 B、±5 C、±
D、
3. 下列计算正确的是（ ）A、
＝﹣2
B、3
＝1
C、
D、3
＝
4. 在下列长度的各组线段中，能组成直角三角形的是（ ）。A、5，6，7 B、5，12，13 C、1，4，9 D、5，11，125. 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”.他们仅仅少走了几步路，却踩伤了花草.他们少走的路长为（ ）
A、2m B、3m C、3.5m D、4m6. 点P的坐标为（a，b），其中a＜0，b＜0，那么点P在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 关于函数y＝﹣x+2有下列结论，其中错误的是（ ）A、图象经过点（1，1） B、若点A（0，y1），B（2，y2）在图象上，则y1＞y2 C、图象向下平移2个单位长度后，图象经过点（0，1） D、当x＞2时，y＜08. 一次函数y＝kx和y＝﹣x+3的图象如图所示，则二元一次方程组的解是（ ）
A、 B、 C、 D、9. 一次函数与 ， 它们在同一坐标系内的图象可能为（ ）A、
B、
C、
D、
10. 已知，如图，直线AB：y=kx-k-4，分别交平面直角坐标系于A，B两点，直线CD.y=-2x+2与坐标轴交于C，D两点，两直线交于点E（a，-a）；点M是y轴上一动点，连接ME，将△AEM沿ME翻折，A点对应点刚好落在x轴负半轴上，则ME所在直线解析式为（ ）
A、y＝
x﹣
B、y＝2x﹣6
C、y＝
x﹣
D、y＝x﹣
二、填空题（每题4分，共28分）
-
11. 27的立方根为 ．12. 比较大小：4
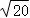（填“＞”“＜”或“＝”）. 13. 已知
是关于x、y的方程2x﹣ay＝3的一个解，则a的值是 . 14. 如图，在数轴上点 A 表示的实数是 ．
15. 若一次函数的图象与直线y＝﹣x+3平行且经过点A（2，0），求其解析式 .16. 如图，矩形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于 ．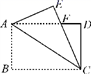
17. 在平面直角坐标系中，直线l与y轴交于点A（0，1），且直线l与x轴相交所成的锐角为45°，如图所示，在直线l上，点C1 ， C2 ， C3 ， C4 ， ⋯⋯在x轴正半轴上，依次作正方形OA1B1C1 ， 正方形C1A2B2C2 ， 正方形C2A3B3C3 ， 正方形C3A4B4C4 ， ⋯⋯点A1 ， A2 ， A3.，A4 ， ⋯⋯则只由前n个正方形所形成图形的周长和是 .（用n的代数式表示）
三、解答题（一）（本大题3小题，每题6分，共18分）
-
18. 计算：(1)、；(2)、；19. 解方程组：
. 20. 如图，在平面直角坐标系中，△ABC顶点分别是A（0，2），B（2，﹣2），C（4，﹣1）.
(1)、在图中作出△ABC关于y轴对称的△A1B1C1；(2)、直接写出对称点坐标B1 ， C1；(3)、在图中第一象限格点中找出点D ， 使AD＝
， 且同时CD＝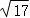
.（无需计算过程，请把点画清楚一些.） 四、解答题（二）（本大题3小题，每题8分，共24分）
-
21. 如图所示的一块地ABCD，已知AD=4m，CD=3m，∠ADC=90°，AB=13m，BC=12m，求这块地的面积．
22. 在一次知识竞赛中，学校为获得一等奖和二等奖共30名学生购买奖品，共花费528元，其中一等奖奖品每件20元，二等奖奖品每件16元，求获得一等奖和二等奖的学生分别有多少名.根据题意列方程组.23. 甲、乙两人分别从A，B两地去同一城市C，他们离A地的路程y（千米）随时间x（时）变化的图象如图所示，根据图象解答下列问题：
(1)、A ， B两地的路程为 千米；(2)、乙离A地的路程y（千米）关于时间x（时）的函数表达式是 .(3)、求当甲、乙两人在途中相遇时离A地的路程？五、解答题（三）（本大题2小题，每题10分，共20分）
x+2的图像与正比例函数y=
