浙江省金华市义乌市三校联考2023-2024学年七年级上学期12月月考数学试题

试卷更新日期：2024-02-02 类型：月考试卷

进入出卷网下载

一、单选题（每小题3分，共30分）

1. 下列方程中，是一元一次方程的是（）

A、 $3 x - 2 y = 1$ B、 $1 + \frac{1}{x} = x$ C、 $x^{2} = 9$ D、 $2 x - 3 = 5$

查看试题解析
2. 2023年10月26日，神州十七号3名宇航员汤洪波、唐胜杰、江新林进入中国空间站，与神十六乘组顺利完成“太空会师”．中国的太空空间站离地球大约400000米，则近似数400000用科学记数法表示，正确的是（）

A、 $4 \times 1 0^{5}$ B、 $40 \times 1 0^{5}$ C、 $40 \times 1 0^{4}$ D、 $0.4 \times 1 0^{6}$

查看试题解析
3. 下列关于单项式 $- \frac{x y^{2}}{3}$ 的说法中，正确的是（）

A、系数是 $- 3$ ，次数是2 B、系数是 $- 3$ ，次数是3 C、系数是 $- \frac{1}{3}$ ，次数是2 D、系数是 $- \frac{1}{3}$ ，次数是3

查看试题解析
4. 在实数 $3.142 ， 0 ， \frac{π}{2} ， - \frac{1}{3} ， 1.01001000100001 \dots$ （两个“1”之间依次多1个“0”）中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若 $a^{2} = 9 ， \sqrt[3]{b} = - 2$ ，则 $a + b =$ （）

A、 $- 5$ 或 $- 11$ B、 $- 5$ C、 $- 11$ D、5或11

查看试题解析

6. 下面是高琪同学做的练习题，她做对了（）道

填空题：

（1） $\sqrt{4}$ 的相反数是 $- 2$ （2）算术平方根等于它本身的数有0和1

（3） $| 3 - π | = 3 - π$ （4） $- \sqrt{\frac{4}{9}}$ 的倒数是 $\frac{3}{2}$

（5）近似数5.2万精确到了千位（6）已知 $\sqrt{a + 1} + | b - 1 | = 0$ ，则 $a + b = 2$

A、5 B、4 C、3 D、2

查看试题解析

7. 某商店有两个进价不同的物品都卖了 $a$ 元，其中一个盈利 $20 %$ ，另一个亏损 $20 %$ ，在这次买卖中，这家商店（）

A、不赔不赚 B、赚了 C、赔了 D、与 $a$ 有关，无法确定

查看试题解析
8. 已知关于 $x$ 的一元一次方程 $\frac{x}{2023} + 5 = 2023 x + 2 a$ 的解为 $x = 4$ ，那么关于 $y$ 的一元一次方程 $\frac{3 - y}{2023} + 2023 (y - 3) = 2 a - 5$ 的解为（）

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
9. 如图，在两个完全相同的大长方形中各放入五个完全一样的白色小长方形，得到图（1）与图（2）．若 $A B = m$ ，则图（1）与图（2）阴影部分周长的差是（）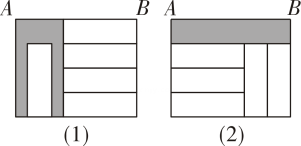

A、 $m$ B、 $\frac{5}{4} m$ C、 $\frac{6}{5} m$ D、 $\frac{7}{6} m$

查看试题解析
10. 如上图，10个人围成一圈做游戏．游戏的规则是：每个人心里都想一个数，并把自己想的数告诉与他相邻的两个人，然后每个人将与他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报出来的数是3的人心里想的数是（）

A、2 B、 $- 2$ C、4 D、 $- 4$

查看试题解析

二、填空题（每小题3分，共18分）

11. 大于 $- 4.5$ 而不大于3的所有整数的积是．

查看试题解析
12. 已知 $7 + \sqrt{14}$ 的小数部分是 $a ， 7 - \sqrt{14}$ 的小数部分是 $b$ ，则 $(a + b)^{2021} =$ ．

查看试题解析
13. 若 $- 6 x^{2} y^{n}$ 与 $2 x^{m + 4} y^{3}$ 的和是单项式，则 $m n$ 的值是．

查看试题解析
14. 已知方程 $\frac{9}{2} x + 6 = 5 + 4 x$ 的解比关于 $x$ 的方程 $7 x - 3 a = 0$ 的解小1，则 $a$ 的值为．

查看试题解析
15. 已知 $2 m^{2} + 2 m n - n^{2} = 1012 ， m n + 2 n^{2} = - 9$ ，则 $4 m^{2} + 5 m n =$ ．

查看试题解析
16. 国家发展改革委表示，今年国庆中秋小长假中，居民消费需求集中释放，进一步巩固了消费回升的好势头．小长假期间，某商场推出回馈消费者的打折活动，具体优惠情况如表：
购物总金额（原价）
折扣
超过300元且不超过500元
全部商品打九折
超过500元且不超过800元
全部商品打八五折
超过800元
全部商品打八折
某市民在该商场购买了一件原价400元的商品 $A$ 和一件原价 $x$ 元的商品 $B$ ，实际付费1006元．则 $x$ 的值可能为（注：两件商品可以单独付款或一起付款）

查看试题解析

三、解答题（本题有8个小题，共52分）

17. 计算：

(1)、 $- 3^{2} - | - 2 | + \sqrt[3]{27}$

(2)、 $(- 12) \times (\frac{1}{6} - \frac{1}{3} - \frac{1}{4}) - {(- \frac{1}{2})}^{2}$

查看试题解析
18. 解方程：

(1)、 $2 x - 7 = - 5 (2 - x)$

(2)、 $\frac{x + 3}{6} = \frac{2 x - 3}{4} + 1$

查看试题解析
19. 先化简，再求值： $3 x - (2 x^{2} - 4 x + 1) + (3 x^{2} - 2 x)$ ，其中 $x = 2$ ．

查看试题解析
20. 有20箱苹果，以每箱15千克为标准，超过15千克的数记为正数，不足15千克的数记为负数，称重记录如下：
与标准质量的差（千克）
$- 0.5$
$- 0.4$
$- 0.2$
0
$+ 0.2$
$+ 0.3$
$+ 0.6$
箱数（箱）
2
1
5
2
4
2
4

(1)、最重的一箱比最轻的一箱重千克；

(2)、求这20箱苹果的总质量；

(3)、若这批苹果的批发价是8.5元/千克，售价是15元/千克，运输和出售过程中有 $10 %$ 的苹果腐烂无法出售，则出售这20箱苹果能盈利多少元？

查看试题解析
21. 规定一种新运算： $(a ， b) ◎ (c ， d) = a d - b c$ ．如 $(1 ， 2) ◎ (3 ， 4) = 1 \times 4 - 2 \times 3 = - 2$ ．

(1)、求 $(5 ， - 3) ◎ (- 1 ， - 2)$ 的值；

(2)、若 $(2 ， x) ◎ (k ， 2 x + k)$ 的值与 $x$ 的取值无关，求有理数 $k$ 的值．

查看试题解析
22. 粤港澳大湾区自动驾驶产业联盟积极推进自动驾驶出租车应用落地工作，无人化是自动驾驶的终极目标．某公交集团拟在今明两年共投资9500万元改装240辆无人驾驶出租车投放市场．今年每辆无人驾驶出租车的改装费用是50万元，预计明年每辆无人驾驶出租车的改装费用可下降 $50 %$ ．

(1)、求明年每辆无人驾驶出租车的预计改装费用是多少万元；

(2)、求明年改装的无人驾驶出租车是多少辆．

查看试题解析

23. 某快递公司规定每件体积不超标的普通小件物品的收费标准如表：

寄往本省内		寄往周边省份
首重	续重	首重	续重
8元/千克	5元/千克	12元/千克	6元/千克
说明：①每件快递按送达地（省内，省外）分别计算运费．②运费计算方式：首重价格+续重×续重运费．首重均为1千克，超过1千克即要续重，续重以0.5千克为一个计重单位（不足0.5千克按0.5千克计算）．

例如：寄往省内一件1.6千克的物品，运费总额为： $8 + 5 \times (0.5 + 0.5) = 13$ 元．寄往省外一件2.3千克的物品，运费总额为： $12 + 6 \times (1 + 0.5) = 21$ 元．（下面问题涉及的寄件按上表收费标准计费）

(1)、小明同时寄往省内一件3千克的物品和省外一件2.8千克的物品，各需付运费多少元？

(2)、小明寄往省内一件重

(m + n)

千克，其中

m

是大于1的正整数，

n

为大于0且不超过0.5的小数（即

0 < n \leq 0.5

），则用含字母

m

的代数式表示小明这次寄件的运费为；

(3)、小明一次向省外寄了一件物品，用了36元，你能知道小明这次寄件物品的重量范围吗？

查看试题解析

24. 数轴上有 $A ， B ， C$ 三个点，分别表示有理数 $- 30 ， - 16 ， 4$ ，两条动线段 $P Q$ 和 $M N ， P Q = 2 ， M N = 3$ ，如图，线段 $M N$ 以每秒1个单位的速度从点 $B$ 开始一直向右匀速运动，线段 $P Q$ 同时以每秒2个单位的速度从点 $A$ 开始向右匀速运动，当点 $Q$ 运动到 $C$ 时，线段 $P Q$ 立即以相同的速度返回，当点 $P$ 运动到点 $A$ 时，线段 $M N ， P Q$ 立即同时停止运动，设运动时间为 $t$ 秒（整个运动过程中，线段 $P Q$ 和 $M N$ 保持长度不变，且点 $P$ 总在点 $Q$ 的左边，点 $M$ 总在点 $N$ 的左边）

(1)、当 $t = 3$ 时，点 $Q$ 表示的数为，点 $M$ 表示的数为．

(2)、当 $t$ 为何值时，点 $Q$ 和点 $N$ 重合？

(3)、在整个运动过程中，线段 $P Q$ 和 $M N$ 重合部分长度能否为1，若能，请求出此时点 $P$ 表示的数；若不能，请说明理由．

查看试题解析

购物总金额（原价）	折扣
超过300元且不超过500元	全部商品打九折
超过500元且不超过800元	全部商品打八五折
超过800元	全部商品打八折

与标准质量的差（千克）	$- 0.5$	$- 0.4$	$- 0.2$	0	$+ 0.2$	$+ 0.3$	$+ 0.6$
箱数（箱）	2	1	5	2	4	2	4